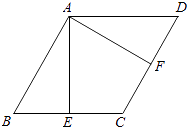
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:由题意可得若 ![]()
![]() =(
=( ![]() +
+ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() +
+ ![]() +
+ ![]() +
+ ![]() =2×2×cos120°+
=2×2×cos120°+ ![]() +λ
+λ ![]()
![]() +λ
+λ ![]() μ
μ ![]() =﹣2+4μ+4λ+λμ×2×2×cos120°
=﹣2+4μ+4λ+λμ×2×2×cos120°
=4λ+4μ﹣2λμ﹣2=1,
∴4λ+4μ﹣2λμ=3 ①.![]()
![]() =﹣
=﹣ ![]() (﹣
(﹣ ![]() )=
)= ![]() =(1﹣λ)
=(1﹣λ) ![]() (1﹣μ)
(1﹣μ) ![]() =(1﹣λ)
=(1﹣λ) ![]() (1﹣μ)
(1﹣μ) ![]()
=(1﹣λ)(1﹣μ)×2×2×cos120°=(1﹣λ﹣μ+λμ)(﹣2)=﹣ ![]() ,
,
即﹣λ﹣μ+λμ=﹣ ![]() ②.
②.
由①②求得λ+μ= ![]() ,
,
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一扇形的周长为20cm,当扇形的圆心角α等于多少时,这个扇形的面积最大?最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
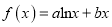 (
(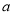 ,
, 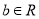 ),
),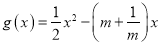 (
(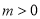 ),且
),且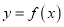 在点
在点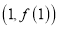 处的切线方程为
处的切线方程为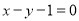 .
.(Ⅰ)求
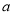 ,
, 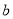 的值;
的值;(Ⅱ)若函数
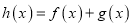 在区间
在区间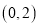 内有且仅有一个极值点,求
内有且仅有一个极值点,求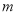 的取值范围;
的取值范围;(Ⅲ)设
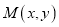 (
(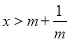 )为两曲线
)为两曲线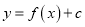 (
(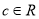 ),
),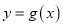 的交点,且两曲线在交点
的交点,且两曲线在交点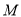 处的切线分别为
处的切线分别为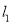 ,
, 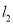 .若取
.若取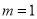 ,试判断当直线
,试判断当直线 ,
,  与
与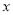 轴围成等腰三角形时
轴围成等腰三角形时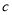 值的个数并说明理由.
值的个数并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cos2x+sin2x﹣4cosx.
(1)求 的值;
的值;
(2)求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
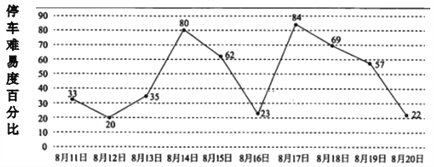
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设
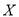 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求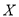 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
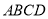 中,
中, 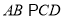 ,
, 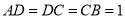 ,
, 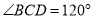 ,四边形
,四边形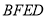 为矩形,平面
为矩形,平面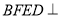 平面
平面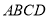 ,
, 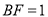 .
.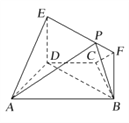
(Ⅰ)求证:
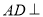 平面
平面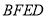 ;
;(Ⅱ)点
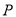 在线段
在线段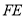 上运动,设平面
上运动,设平面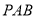 与平面
与平面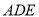 所成锐二面角为
所成锐二面角为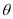 ,试求
,试求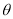 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量
48
49
50
51
天数
20
40
20
20
乙口味糕点日销量
48
49
50
51
天数
40
30
20
10
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
相关试题

