【题目】已知椭圆C: ![]() =1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
=1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 ![]() b.
b.
(1)求椭圆C的离心率;
(2)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
参考答案:
【答案】
(1)解:设F的坐标为(﹣c,0),依题意有bc= ![]() ab,
ab,
∴椭圆C的离心率e= ![]() =
= ![]() .
.
(2)解:若b=2,由(1)得a=2 ![]() ,∴椭圆方程为
,∴椭圆方程为 ![]() .
.
联立方程组 ![]()
化简得:(2k2+1)x2+16kx+24=0,
由△=32(2k2﹣3)>0,解得:k2> ![]()
由韦达定理得:xM+xN= ![]() …①,xMxN=
…①,xMxN= ![]() …②
…②
设M(xM,kxM+4),N(xN,kxN+4),
MB方程为:y= ![]() x﹣2,…③
x﹣2,…③
NA方程为:y= ![]() x+2,…④
x+2,…④
由③④解得:y= ![]()
= 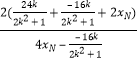 =
= 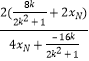 =1
=1
即yG=1,
∴直线BM与直线AN的交点G在定直线上
【解析】(1)设F的坐标为(﹣c,0),原点O到直线FA的距离为 ![]() b,列出方程,即可求解椭圆的离心率.(2)求出椭圆方程,联立方程组
b,列出方程,即可求解椭圆的离心率.(2)求出椭圆方程,联立方程组 ![]() ,通过韦达定理,设M(xM , kxM+4),N(xN , kxN+4),
,通过韦达定理,设M(xM , kxM+4),N(xN , kxN+4),
求出MB方程,NA方程,求出交点坐标,推出结果.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
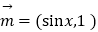 ,
,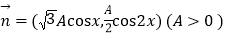 ,函数
,函数 的最大值为
的最大值为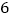 .
.
(1)求
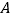 的大小;
的大小;(2)将函数
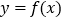 的图象向左平移
的图象向左平移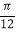 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数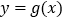 的图象,作出函数
的图象,作出函数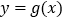 在
在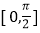 的图象.
的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
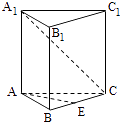
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若关于
 的不等式
的不等式 恒成立,求整数
恒成立,求整数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
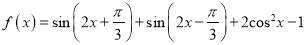 ,
, 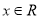 .
.(1)求函数
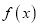 的最小正周期;
的最小正周期;(2)求函数
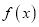 在区间
在区间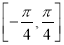 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品,根据经验知道,次品数P(万件)与日产量x(万件)之间满足关系:
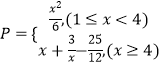 已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
(1)试将该工厂每天生产这种元件所获得的利润T(万元)表示为日产量x(万件)的函数;
(2)当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大,最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入) 问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
相关试题

