【题目】如图,直三棱柱![]() 中,
中,![]() 且
且![]() ,
,![]() 是棱
是棱![]() 上的动点,
上的动点,![]() 是
是![]() 的中点.
的中点.
(1)当![]() 是
是![]() 中点时,求证:
中点时,求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,若存在,求
,若存在,求![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】【试题分析】(1)取![]() 中点
中点![]() ,连结
,连结![]() ,利用三角形中位线证得四边形
,利用三角形中位线证得四边形![]() 为平行四边形,由此证得线面平行.(2)假设存在这样的点
为平行四边形,由此证得线面平行.(2)假设存在这样的点![]() ,以
,以![]() 点为原点建立空间直角坐标系,利用平面
点为原点建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,结合它们所成锐二面角的余弦值,可求得这个点的坐标.
的法向量,结合它们所成锐二面角的余弦值,可求得这个点的坐标.
【试题解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ∥
∥![]() 且
且![]() .
.
因为当![]() 为
为![]() 中点时,
中点时,![]() ∥
∥![]() 且
且![]() ,
,
所以![]() ∥
∥![]() 且
且![]()
![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,![]() ∥
∥![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)假设存在满足条件的点![]() ,设
,设![]() .
.
以![]() 为原点,向量
为原点,向量![]() 方向为
方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立空间直角坐标系.
轴正方向,建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
平面![]() 的法向量
的法向量![]() ,
, ,
,
解得![]() ,所以存在满足条件的点
,所以存在满足条件的点![]() ,此时
,此时![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟



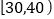


总人数
20
36
44
50
40
10
将学生日均课外体育锻炼时间在
 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面的
 列联表;
列联表;课外体育不达标
课外体育达标
合计
男
女
20
110
合计
(2)通过计算判断是否能在犯错误的概率不超过
 的前提下认为“课外体育达标”性别有关?
的前提下认为“课外体育达标”性别有关?参考公式
 ,其中
,其中

0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
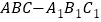 中,
中,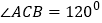 且
且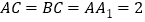 ,
,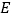 是棱
是棱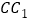 上的动点,
上的动点,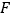 是
是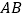 的中点.
的中点.(1)当
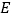 是
是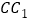 中点时,求证:
中点时,求证: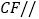 平面
平面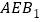 ;
;(2)在棱
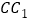 上是否存在点
上是否存在点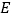 ,使得平面
,使得平面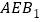 与平面
与平面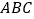 所成锐二面角为
所成锐二面角为 ,若存在,求
,若存在,求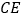 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.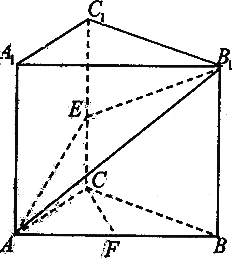
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均课外体育锻炼时间在
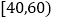 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面的
 列联表;
列联表;课外体育不达标
课外体育达标
合计
男
女
20
110
合计
(2)通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
参考格式:
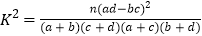 ,其中
,其中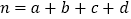

0.025
0.15
0.10
0.005
0.025
0.010
0.005
0.001

5.024
2.072
6.635
7.879
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农民户籍各50人;男性60人,女性40人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
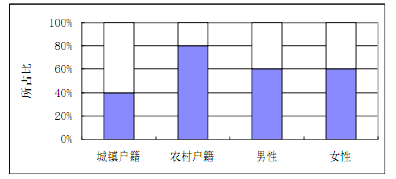
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别无关
C. 倾向选择生育二胎的人员中,男性人数与女性人数相同
D. 倾向选择生育二的人员中,农村户籍人数少于城镇户籍人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
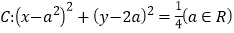 ,考虑下列命题:①圆
,考虑下列命题:①圆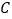 上的点到
上的点到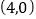 的距离的最小值为
的距离的最小值为 ;②圆
;②圆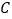 上存在点
上存在点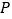 到点
到点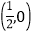 的距离与到直线
的距离与到直线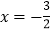 的距离相等;③已知点
的距离相等;③已知点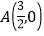 ,在圆
,在圆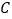 上存在一点
上存在一点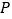 ,使得以
,使得以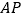 为直径的圆与直线
为直径的圆与直线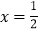 相切,其中真命题的个数为( )
相切,其中真命题的个数为( )A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容易.”这里的“幂”指水平截面的面积.“势”指高,这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。于是可把半径相等的半球(底面在下)和圆柱(圆柱高等于半径)放在同一水平面上,圆柱里再放一个半径和高都与圆柱相等的圆锥(锥尖朝下),考察圆柱里被圆锥截剩的立体,这样在同一高度用平行平面截得的半球截面和圆柱中剩余立体截得的截面面积相等,因此半球的体积等于圆柱中剩余立体的体积.设由椭圆
 所围成的平面图形绕
所围成的平面图形绕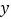 轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.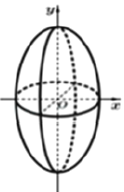
相关试题

