【题目】已知函数,
(1)求![]() 在区间
在区间![]() 上的极小值和极大值;
上的极小值和极大值;
(2)求![]() 在
在![]() (
(![]() 为自然对数的底数)上的最大值.
为自然对数的底数)上的最大值.
参考答案:
【答案】(1)极小值为![]() ,极大值为
,极大值为![]() .(2)答案不唯一,具体见解析
.(2)答案不唯一,具体见解析
【解析】
(1)对三次函数![]() 进行求导,解导数不等式,画出表格,从而得到极值;
进行求导,解导数不等式,画出表格,从而得到极值;
(2)由(1)知函数![]() 的性质,再对
的性质,再对![]() 进行分类讨论,求
进行分类讨论,求![]() 在
在![]() 的性质,比较两段的最大值,进而得到函数
的性质,比较两段的最大值,进而得到函数![]() 的最大值.
的最大值.
(1)当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() .当x变化时,
.当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
x |
| 0 |
|
|
|
| - | 0 | + | 0 | - |
| 递减 | 极小值 | 递增 | 极大值 | 递减 |
故当![]() 时,函数
时,函数![]() 取得极小值为
取得极小值为![]() ,
,
当![]() 时,函数
时,函数![]() 取值极大值为
取值极大值为![]() .
.
(2)①当![]() 时,由(1)知,
时,由(1)知,
函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上的值大值为2.
上的值大值为2.
②当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
故当![]() 时,
时,![]() 在
在![]() 上最大值为
上最大值为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上的最大值为2.
上的最大值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某有机水果种植基地试验种植的某水果在售卖前要成箱包装,每箱80个,每一箱水果在交付顾客之前要按约定标准对水果作检测,如检测出不合格品,则更换为合格品.检测时,先从这一箱水果中任取10个作检测,再根据检测结果决定是否对余下的所有水果作检测.设每个水果为不合格品的概率都为
 ,且各个水果是否为不合格品相互独立.
,且各个水果是否为不合格品相互独立.(Ⅰ)记10个水果中恰有2个不合格品的概率为
 ,求
,求 取最大值时p的值
取最大值时p的值 ;
;(Ⅱ)现对一箱水果检验了10个,结果恰有2个不合格,以(Ⅰ)中确定的
 作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用
作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用 .
.(ⅰ)若不对该箱余下的水果作检验,这一箱水果的检验费用与赔偿费用的和记为X,求EX;
(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,当种植基地要对每个不合格水果支付的赔偿费用至少为多少元时,将促使种植基地对这箱余下的所有水果作检验?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A. (-∞,0) B.
 C. (0,1) D. (0,+∞)
C. (0,1) D. (0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩
 、物理成绩
、物理成绩 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.数学
88
83
117
92
108
100
112
物理
94
91
108
96
104
101
106
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩
 与数学成绩
与数学成绩 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.参考公式:方差公式:
 ,其中
,其中 为样本平均数.
为样本平均数. ,
, 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若对于
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)若对于
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 为山脚两侧共线的3点,在山顶
为山脚两侧共线的3点,在山顶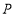 处测得3点的俯角分别为
处测得3点的俯角分别为 ,计划沿直线
,计划沿直线 开通穿山隧道,为求出隧道
开通穿山隧道,为求出隧道 的长度,你认为还需要直接测量出
的长度,你认为还需要直接测量出 中哪些线段的长度?根据条件,并把你认为需要测量的线段长度作为已知量,写出计算隧道
中哪些线段的长度?根据条件,并把你认为需要测量的线段长度作为已知量,写出计算隧道 长度的运算步骤.
长度的运算步骤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,则关于
,则关于 的方程
的方程 ,给出下列五个命题:①存在实数
,给出下列五个命题:①存在实数 ,使得该方程没有实根;
,使得该方程没有实根;②存在实数
 ,使得该方程恰有
,使得该方程恰有 个实根;
个实根;③存在实数
 ,使得该方程恰有
,使得该方程恰有 个不同实根;
个不同实根; ④存在实数
 ,使得该方程恰有
,使得该方程恰有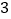 个不同实根;
个不同实根;⑤存在实数
 ,使得该方程恰有
,使得该方程恰有 个不同实根.
个不同实根.其中正确的命题的个数是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

