【题目】选修4-4:坐标系与参数方程
在极坐标系中,点![]() ,曲线
,曲线 ![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.
(1)在直角坐标系中,求点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1), 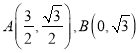
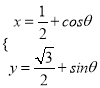 (
(![]() ,
, ![]() 为参数);(2)
为参数);(2) ![]() .
.
【解析】试题分析:
(1)由公式![]() 可化点的极坐标为直角坐标,也可化曲线的极坐标方程为直角坐标方程,由直角坐标方程知曲线
可化点的极坐标为直角坐标,也可化曲线的极坐标方程为直角坐标方程,由直角坐标方程知曲线![]() 是圆,且圆心坐标与半径都已知,可由圆的标准参数方程可得;
是圆,且圆心坐标与半径都已知,可由圆的标准参数方程可得;
(2)利用参数方程设出![]() 点坐标,由两点间距离公式求得
点坐标,由两点间距离公式求得![]() ,应用两角和与差的正弦公式化表达式为
,应用两角和与差的正弦公式化表达式为![]() 形式,再结合正弦函数性质可得取值范围.
形式,再结合正弦函数性质可得取值范围.
试题解析:
(1)由![]() ,解得
,解得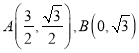 ,
,
因为![]() ,所以,
,所以, 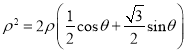 ,即
,即![]()
即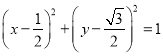 ,
,
所以曲线![]() 的参数方程为:
的参数方程为:  (
(![]() ,
, ![]() 为参数);
为参数);
(2)不妨设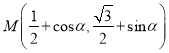 ,
,
则
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因此, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
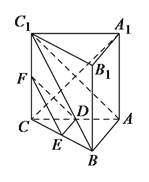
查看答案和解析>>【题目】如图,在三棱柱
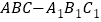 中,
中,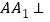 底面
底面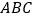 ,
,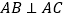
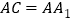 ,
,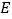 、
、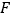 分别是棱
分别是棱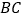 、
、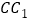 的中点.
的中点.(Ⅰ)求证:
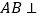 平面
平面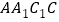 .
.(Ⅱ)若线段
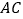 上的点
上的点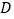 满足平面
满足平面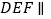 平面
平面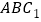 ,试确定点
,试确定点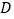 的位置,并说明理由.
的位置,并说明理由.(Ⅲ)证明:
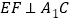 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在
 市的
市的 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记 表示在各区开设分店的个数,
表示在各区开设分店的个数,  表示这个
表示这个 个分店的年收入之和.
个分店的年收入之和. (个)
(个)2
3
4
5
6
 (百万元)
(百万元)2.5
3
4
4.5
6
(1)该公司已经过初步判断,可用线性回归模型拟合
 与
与 的关系,求
的关系,求 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)假设该公司在
 区获得的总年利润
区获得的总年利润 (单位:百万元)与
(单位:百万元)与 之间的关系为
之间的关系为 ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在 区开设多少个分时,才能使
区开设多少个分时,才能使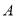 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?(参考公式:
 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差不为零,a1=25,且a1 , a11 , a13成等比数列.
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点

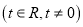 为圆心的圆与
为圆心的圆与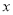 轴交于点
轴交于点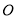 、
、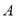 ,与
,与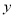 轴交于点
轴交于点 、
、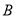 ,其中
,其中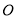 为原点.
为原点.(
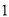 )求证:
)求证: 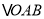 的面积为定值.
的面积为定值.(
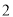 )设直线
)设直线 与圆
与圆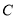 交于点
交于点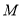 、
、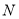 ,若
,若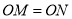 ,求:圆
,求:圆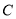 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
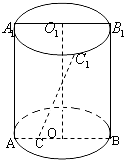
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC=  OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三棱柱
 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 面
面 ,
,  是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.(
 )求证:
)求证:  平面
平面 .
.(
 )求证:
)求证:  .
.
相关试题

