【题目】如图,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)探究在![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由.
,并说明理由.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)连结![]() ,由几何体的空间结构可证得
,由几何体的空间结构可证得![]() ,利用线面垂直的定义可知
,利用线面垂直的定义可知![]() .
.
(2)由(1)知![]() 为腰长为1的等腰直角三角形,结合题意转化顶点可得
为腰长为1的等腰直角三角形,结合题意转化顶点可得![]() .
.
(3)在![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .取
.取![]() 的中点
的中点![]() ,连结
,连结![]() . 易证得四边形EGHC是平行四边形,所以EG//CH,结合线面平行的判断定理可知EG//平面PCD.
. 易证得四边形EGHC是平行四边形,所以EG//CH,结合线面平行的判断定理可知EG//平面PCD.
(1)连结![]() ,∵
,∵![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,同理可得
,同理可得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,且
,且![]() , ∴
, ∴![]() ,
,
又∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
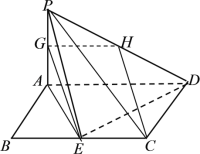
(2)由(1)知![]() 为腰长为1的等腰直角三角形,
为腰长为1的等腰直角三角形,
∴![]() ,而
,而![]() 是三棱锥
是三棱锥![]() 的高,
的高,
∴![]() .
.
(3)在![]() 上存在中点
上存在中点![]() ,使得
,使得![]() .理由如下:
.理由如下:
取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
∵![]() 是
是![]() 的中点, ∴
的中点, ∴![]() ,且
,且![]() ,
,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=![]() AD,
AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG![]() 平面PCD,CH
平面PCD,CH![]() 平面PCD,所以EG//平面PCD.
平面PCD,所以EG//平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较注射
 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物 ,另一组注射药物
,另一组注射药物 .
. (1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)下表1和表2分别是注射药物
 和
和 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: 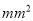 )
) 表1:注射药物
 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
表2:注射药物
 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
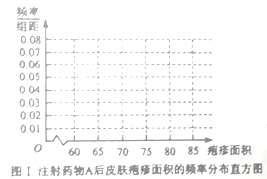
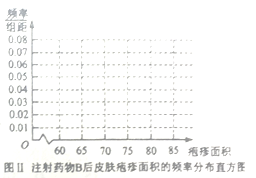
(ⅱ)完成下面
 列联表,并回答能否有
列联表,并回答能否有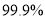 的把握认为“注射药物
的把握认为“注射药物 后的疱疹面积与注射药物
后的疱疹面积与注射药物 后的疱疹面积有差异”.
后的疱疹面积有差异”.表3:

附:
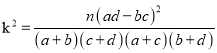
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直三棱柱
 的所有棱长都相等,且
的所有棱长都相等,且 ,
,  ,
, 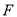 ,分别为
,分别为 ,
,  ,
,  的中点.
的中点.(1)求证:平面
 平面
平面 .
.(2)求证:
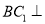 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设过抛物线
 的焦点
的焦点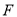 的直线
的直线 交抛物线于点
交抛物线于点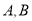 ,若以
,若以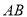 为直径的圆过点
为直径的圆过点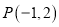 ,且与
,且与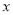 轴交于
轴交于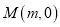 ,
, 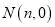 两点,则
两点,则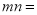 ( )
( )A. 3 B. 2 C. -3 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
,  是非零向量,则“
是非零向量,则“  ,
,  共线”是“|
共线”是“|  |+|
|+|  |=|
|=|  +
+  |”的( )
|”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.(
 )求
)求 的顶点
的顶点 、
、 的坐标.
的坐标.(
 )若圆
)若圆 经过不同的三点
经过不同的三点 、
、 、
、 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,求圆
,求圆 的方程.
的方程.
相关试题

