【题目】设 ![]() ,
, ![]() 是非零向量,则“
是非零向量,则“ ![]() ,
, ![]() 共线”是“|
共线”是“| ![]() |+|
|+| ![]() |=|
|=| ![]() +
+ ![]() |”的( )
|”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
参考答案:
【答案】B
【解析】解:若 ![]() ,
, ![]() 共线,则
共线,则 ![]() =m
=m ![]() ,但m>0时,满足“|
,但m>0时,满足“| ![]() |+|
|+| ![]() |=|
|=| ![]() +
+ ![]() |”,当m<0时,“|
|”,当m<0时,“| ![]() |+|
|+| ![]() |>|
|>| ![]() +
+ ![]() |”,则充分性不成立, 反之若“|
|”,则充分性不成立, 反之若“| ![]() |+|
|+| ![]() |=|
|=| ![]() +
+ ![]() |”,平方得“|
|”,平方得“| ![]() |2+|
|2+| ![]() |2+2|
|2+2| ![]() ||
|| ![]() |=|
|=| ![]() |2+|
|2+| ![]() |2+2
|2+2 ![]()
![]() ”,
”,
即| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |cos<
|cos< ![]() ,
, ![]() >,则cos<
>,则cos< ![]() ,
, ![]() >=1,则<
>=1,则< ![]() ,
, ![]() >=0,即
>=0,即 ![]() ,
, ![]() 共线,即必要性成立,
共线,即必要性成立,
则“ ![]() ,
, ![]() 共线”是“|
共线”是“| ![]() |+|
|+| ![]() |=|
|=| ![]() +
+ ![]() |”的必要不充分条件,
|”的必要不充分条件,
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直三棱柱
 的所有棱长都相等,且
的所有棱长都相等,且 ,
,  ,
, 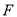 ,分别为
,分别为 ,
,  ,
,  的中点.
的中点.(1)求证:平面
 平面
平面 .
.(2)求证:
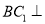 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 为矩形,且
为矩形,且 平面
平面 ,
,  ,
, 为
为 的中点.
的中点.
(1)求证:
 ;
;(2)求三棱锥
 的体积;
的体积;(3)探究在
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ,并说明理由.
,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设过抛物线
 的焦点
的焦点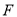 的直线
的直线 交抛物线于点
交抛物线于点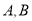 ,若以
,若以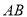 为直径的圆过点
为直径的圆过点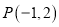 ,且与
,且与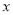 轴交于
轴交于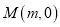 ,
, 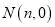 两点,则
两点,则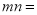 ( )
( )A. 3 B. 2 C. -3 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.(
 )求
)求 的顶点
的顶点 、
、 的坐标.
的坐标.(
 )若圆
)若圆 经过不同的三点
经过不同的三点 、
、 、
、 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,求圆
,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点的椭圆
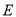 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 的焦点,且椭圆
的焦点,且椭圆 的离心率是
的离心率是 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 的动直线与椭圆
的动直线与椭圆 相交于
相交于 两点.若线段
两点.若线段 的中点的横坐标是
的中点的横坐标是 ,求直线
,求直线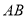 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
 为圆心的圆经过点
为圆心的圆经过点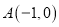 和
和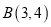 ,线段
,线段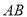 的垂直平分线交圆
的垂直平分线交圆 于点
于点 和
和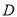 ,且
,且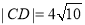 .
.(1)求直线
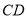 的方程;
的方程;(2)求圆
 的方程;
的方程;(3)设点
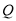 在圆
在圆 上,试问使△
上,试问使△ 的面积等于8的点
的面积等于8的点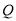 共有几个?证明你的结论.
共有几个?证明你的结论.
相关试题

