【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值与曲线在点
的值与曲线在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,且当
,且当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最大值.(
的最大值.(![]() )
)
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)求导,利用导数的几何意义和两直线垂直的判定求出![]() 值,进而利用点斜式方程进行求解;(Ⅱ)分离参数,合理构造函数,将问题转化为求函数的最值问题,再利用导数研究函数的单调性和最值.
值,进而利用点斜式方程进行求解;(Ⅱ)分离参数,合理构造函数,将问题转化为求函数的最值问题,再利用导数研究函数的单调性和最值.
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() ,
, ![]() .
.
又曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,故
垂直,故![]() ,解得
,解得![]() ,
,
所以![]() ,
, ![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(Ⅱ)当![]() 时,
时, ![]() 恒成立等价于
恒成立等价于![]() 恒成立,等价于当
恒成立,等价于当![]() 时,
时, ![]() 恒成立.
恒成立.
设![]() (
(![]() ),则
),则![]() ,记
,记![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上存在唯一的实数根
上存在唯一的实数根![]() ,使得
,使得![]() ,①
,①
因此当![]() 时,
时, ![]() ,即
,即![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,即
,即![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时, ![]() ,由①可得
,由①可得![]() ,
,
所以![]() .
.
因为![]() ,
, ![]() ,又
,又![]() ,
, ![]() ,
,
所以![]() ,因此
,因此![]() ,
,
又![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y=
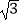 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 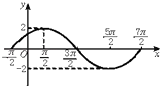
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知cosx=﹣
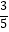 ,x∈(0,π)
,x∈(0,π)
(1)求cos(x﹣ )的值;
)的值;
(2)求sin(2x+ )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
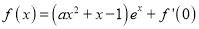 .
. (1)讨论函数
 的单调性;
的单调性;(2)若
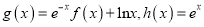 ,过
,过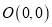 分别作曲线
分别作曲线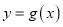 与
与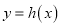 的切线
的切线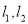 ,且
,且 与
与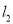 关于
关于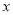 轴对称,求证:
轴对称,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了
 人,得如下所示的列联表:
人,得如下所示的列联表:赞成“自助游”
不赞成“自助游”
合计
男性

女性

合计

(1)若在
 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为 的样本,女性应抽
的样本,女性应抽 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取
 人赠送精美纪念品,记这
人赠送精美纪念品,记这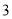 人中赞成“自助游”人数为
人中赞成“自助游”人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:

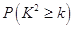









-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
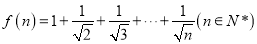 ,
,  .
.(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
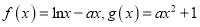 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)讨论函数
 在区间
在区间 上的单调性;
上的单调性;(2)已知
 ,若对任意
,若对任意 ,有
,有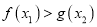 ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

