【题目】已知圆C1的圆心在坐标原点O,且恰好与直线![]() 相切.
相切.
(Ⅰ)求圆C1的标准方程;
(Ⅱ)设点A为圆上一动点,AN垂直于x轴于点N,若动点Q满足![]()
(其中m为非零常数),试求动点Q的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当m=![]() 时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
参考答案:
【答案】(Ⅰ) 圆C1的方程为x2+y2=4;(Ⅱ) 点Q的轨迹方程为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】分析:(Ⅰ)由题意首先求得圆的半径为r=2,结合圆心坐标可得圆C1的方程为x2+y2=4.
(Ⅱ)设动点Q(x,y),A(x0,y0),由题意可得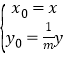 ,则动点Q的轨迹方程为
,则动点Q的轨迹方程为![]() .
.
(Ⅲ)由题意结合(Ⅱ)的结论可知曲线C的方程为![]() ,联立直线方程与椭圆方程可得7x2-8bx+4b2-12=0.结合韦达定理和弦长公式可得面积函数为:
,联立直线方程与椭圆方程可得7x2-8bx+4b2-12=0.结合韦达定理和弦长公式可得面积函数为:![]() ,则△OBD面积的最大值为
,则△OBD面积的最大值为![]() .
.
详解:(Ⅰ)设圆的半径为r,圆心到直线l1的距离为d,
则d=![]() =2.
=2.
因为r=d=2,圆心为坐标原点O,
所以圆C1的方程为x2+y2=4.
(Ⅱ)设动点Q(x,y),A(x0,y0),
∵AN⊥x轴于点N,∴N(x0,0),
由题意知,(x,y)=m(x0,y0)+(1-m)·(x0,0),
解得![]() 即
即![]()
将点A![]() 代入圆C1的方程x2+y2=4,
代入圆C1的方程x2+y2=4,
得动点Q的轨迹方程为![]() +
+![]() =1.
=1.
(Ⅲ)当m=![]() 时,曲线C的方程为
时,曲线C的方程为![]() +
+![]() =1,
=1,
设直线l的方程为y=-x+b,直线l与椭圆![]() +
+![]() =1交点B(x1,y1),D(x2,y2),
=1交点B(x1,y1),D(x2,y2),
联立方程![]() 得7x2-8bx+4b2-12=0.
得7x2-8bx+4b2-12=0.
因为Δ=48(7-b2)>0,
解得b2<7,且x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
又因为点O到直线l的距离d1=![]() ,
,
|BD|=![]() ·
·![]() =
=![]()
![]() .
.
所以S△OBD=![]() ·
·![]() ·
·![]()
![]()
=![]()
![]() ≤
≤![]() ,
,
当且仅当b2=7-b2,
即b2=![]() <7时取到最大值.
<7时取到最大值.
所以△OBD面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
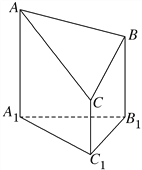
(Ⅰ)该几何体的体积;
(Ⅱ)截面ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 方程
方程  有两个不等的负根,
有两个不等的负根,  方程
方程  无实根,若“
无实根,若“  ”为真,“
”为真,“  ”为假,求实数
”为假,求实数  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)在 中,
中,  分别为内角
分别为内角  的对边,且
的对边,且 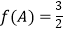 ,
,  ,求
,求  的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如下柱状图:

(1)从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分的概率;
(2)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记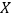 表示两人打分之和,求
表示两人打分之和,求 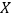 的分布列和
的分布列和 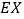 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
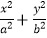 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 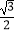 ,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2
,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2 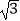 .
.
(1)求椭圆C的方程;
(2)过点D(0,﹣2)作直线l与椭圆C交于A、B两点,点N满足 (O为原点),求四边形OANB面积的最大值,并求此时直线l的方程.
(O为原点),求四边形OANB面积的最大值,并求此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: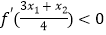 ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记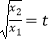 ,求(t﹣1)(a+
,求(t﹣1)(a+ 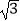 )的值.
)的值.
相关试题

