【题目】(本小题满分12分)
已知函数![]() ,
,![]() 且
且![]() .
.
(Ⅰ)求![]() 的定义域;
的定义域;
(Ⅱ)判断![]() 的奇偶性并予以证明;
的奇偶性并予以证明;
(Ⅲ)当![]() 时,求使
时,求使![]() 的
的![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)解: ∵![]() ,
,
∴![]() 2分
2分
解得![]() . 4分
. 4分
故所求定义域为![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)由(Ⅰ)知![]() 的定义域为
的定义域为![]() ,
,
且![]() 7分
7分
![]()
![]() , 9分
, 9分
故![]() 为奇函数. ………………………………………………………………10分
为奇函数. ………………………………………………………………10分
(Ⅲ)因为f(x)>0,
所以loga(x+1)-loga(1-x)>0,即loga(x+1)>loga(1-x) 12分
因为当![]() 时,y=logax在(0,+)内是增函数,
时,y=logax在(0,+)内是增函数,
所以x+1>1-x,所以x>0, 13分
又![]() 的定义域为
的定义域为![]() ,所以
,所以![]() .
.
所以使![]() 的
的![]() 的取值范围是
的取值范围是![]() . ……………………14分
. ……………………14分
【解析】
解: (Ⅰ)![]() ,则
,则
![]() 解得
解得![]() .
.
故所求定义域为![]() .…………………………………4分
.…………………………………4分
(Ⅱ)由(Ⅰ)知![]() 的定义域为
的定义域为![]() ,
,
且![]()
![]()
![]() ,
,
故![]() 为奇函数. ………………………………………………9分
为奇函数. ………………………………………………9分
(Ⅲ)因为当![]() 时,
时,![]() 在定义域
在定义域![]() 内是增函数,
内是增函数,
所以![]() .
.
解得![]() .
.
所以使![]() 的
的![]() 的取值范围是
的取值范围是![]() .…………………12分
.…………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线
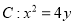 ,过点
,过点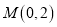 任作一直线与
任作一直线与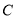 相交于
相交于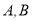 两点,过点
两点,过点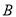 作
作 轴的平行线与直线
轴的平行线与直线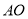 相交于点
相交于点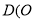 为坐标原点).
为坐标原点).(1)证明: 动点
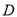 在定直线上;
在定直线上;(2)作
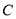 的任意一条切线
的任意一条切线 (不含
(不含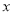 轴), 与直线
轴), 与直线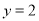 相交于点
相交于点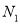 与(1)中的定直线相交于点
与(1)中的定直线相交于点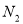 .
.证明:
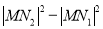 为定值, 并求此定值.
为定值, 并求此定值.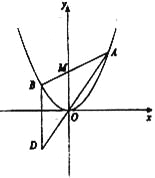
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆
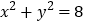 内有一点P(-1,2),AB为过点P且倾斜角为
内有一点P(-1,2),AB为过点P且倾斜角为 的弦.
的弦.(1)当
 时,求AB的长;
时,求AB的长;(2)当弦AB被点P平分时,写出直线AB的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|
 |;
|;(2)已知点D是AB上一点,满足
 =λ
=λ ,点E是边CB上一点,满足
,点E是边CB上一点,满足 =λ
=λ .
.①当λ=
 时,求
时,求
 ;
;②是否存在非零实数λ,使得
 ⊥
⊥ ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为
 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中 ,若
,若 ,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )
,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)求函数y=2|x﹣1|﹣|x﹣4|的值域;
(2)若不等式2|x﹣1|﹣|x﹣a|≥﹣1在x∈R上恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

