【题目】已知函数 ![]() 处都取得极值.
处都取得极值.
(1)求a,b的值;
(2)求f(x)的单调区间.
参考答案:
【答案】
(1)解:由已知可得f'(x)=3x2+2ax+b,
由 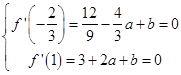
可得 ![]() ;
;
(2)解:由(1)知f'(x)=3x2﹣x﹣2=(3x+2)(x﹣1),
由 ![]() .列表如下:
.列表如下:
x |
|
|
| 1 | (1,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 增 | 极大 | 减 | 极小 | 增 |
所以函数f(x)的递增区间为 ![]() 与(1,+∞),递减区间为
与(1,+∞),递减区间为 ![]()
【解析】(1)求出函数的导数,得到关于a,b的方程组,解出即可求出a,b的值;(2)解关于导函数的不等式,从而求出函数的单调区间.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+
 ax2﹣2x存在单调递减区间,则实数a的取值范围为 .
ax2﹣2x存在单调递减区间,则实数a的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)将根式化为分式指数幂的形式
 ;
;(2)若
 求
求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;患三高疾病
不患三高疾病
合计
男
6
30
女
合计
36
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
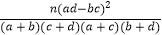 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 有如下性质:该函数在
有如下性质:该函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.(1)已知
 ,利用上述性质,求函数
,利用上述性质,求函数 的单调区间和值域;
的单调区间和值域;(2)对于(1)中的函数
 和函数
和函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足 =
= +
+ =1.
=1.(1)求证:
 =3;
=3;(2)求不等式
 >3的解集.
>3的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
 ;
;(2)
 .
.
相关试题

