
【题目】一批用于手电筒的电池,每节电池的寿命服从正态分布![]() (寿命单位:小时).考虑到生产成本,电池使用寿命在
(寿命单位:小时).考虑到生产成本,电池使用寿命在![]() 内是合格产品.
内是合格产品.
(1)求一节电池是合格产品的概率(结果四舍五入,保留一位小数);
(2)根据(1)中的数据结果,若质检部门检查4节电池,记抽查电池合格的数量为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望及方差.
的分布列、数学期望及方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次53.5公里的自行车个人赛中,25名参赛手的成绩(单位:分钟)的茎叶图如图所示,现将参赛选手按成绩由好到差编为1-25号,再用系统抽样方法从中选取5人.已知选手甲的成绩为85分钟,若甲被选取,则被选取的其余4名选手的成绩的平均数为( )

A. 97 B. 96 C. 95 D. 98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成如下的频率分布直方图;

(2)组委会决定在5名(其中第3组2名,第4组2名,第5组1名)选手中随机抽取2名选手接受![]() 考官进行面试,求第4组至少有1名选手被考官
考官进行面试,求第4组至少有1名选手被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: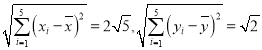
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: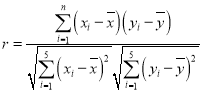 ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
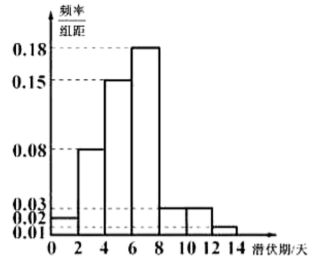
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下表格.
(i)请将表格补充完整;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com