【题目】已知数列![]() 满足
满足![]()
![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)![]() 是以
是以![]() 为首项,2为公差的等差数列 (2)
为首项,2为公差的等差数列 (2)![]()
【解析】试题分析:(1)由 ![]() 可得
可得![]() ,两式相减可得
,两式相减可得![]() ,由等差数列可得结果;(2)由1) 可得
,由等差数列可得结果;(2)由1) 可得![]() ,根据错位相减法可得数列
,根据错位相减法可得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)![]() ....................... ①
....................... ①
![]() 时,
时, ![]() ………………. ②
………………. ②
①-②得![]() ,
,
从而![]()
又![]() 时,
时, ![]()
因此,数列![]() 是以
是以![]() 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.
![]()
(2)![]()
![]() ……………. ③
……………. ③
![]() ……… ④
……… ④
③-④得![]()
整理得 ![]()
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过100km/h的有40人,不超过100km/h的有15人.在45名女性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有25人.
(1)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关.
平均车速超过
100km/h人数
平均车速不超过
100km/h人数
合计
男性驾驶员人数
女性驾驶员人数
合计
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为
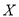 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求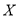 的分布列和数学期望.
的分布列和数学期望.参考公式与数据:
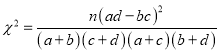 ,其中
,其中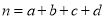
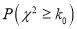
0.150
0.100
0.050
0.025
0.010
0.005
0.001
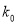
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点C为圆心的圆经过点A(-1,0)和B(3,4),且圆心在直线x+3y-15=0上.设点P在圆C上,求△PAB的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分15分)在直三棱柱
 中,底面
中,底面 是边长为2的正三角形,
是边长为2的正三角形, 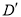 是棱
是棱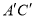 的中点,且
的中点,且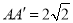 .
.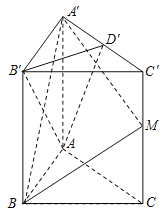
(1)试在棱
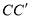 上确定一点
上确定一点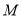 ,使
,使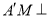 平面
平面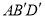 ;
;(2)当点
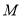 在棱
在棱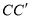 中点时,求直线
中点时,求直线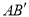 与平面
与平面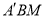 所成角的大小的正弦值。
所成角的大小的正弦值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
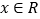 ,用符号
,用符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则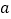 的取值范围是( )
的取值范围是( )A.
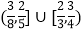 B.
B. 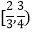
C.
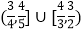 D.
D. 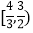
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是
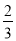 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过下列两点的直线的斜率是否存在?如果存在,求其斜率,并确定直线的倾斜角α.
(1)A(2,3),B(4,5);
(2)C(-2,3),D(2,-1);
(3)P(-3,1),Q(-3,10).
相关试题

