【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若当![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象的上方,求实数
的图象的上方,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】
试题分析:(1)对函数![]() 进行求导,
进行求导,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,得单调区间;(2)将函数
,得单调区间;(2)将函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象的上方转化为不等式
的图象的上方转化为不等式![]() 在
在![]() 上恒成立.
上恒成立.
试题解析:(1)因为![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,
因为当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由当![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象的上方,
的图象的上方,
可得不等式![]() 在
在![]() 上恒成立.
上恒成立.
设![]() ,
,
则![]()
①当![]() 时,因为
时,因为![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上是增函数,又因为
上是增函数,又因为![]() ,所以当
,所以当![]() 时,总有
时,总有![]() ,不符合题意.
,不符合题意.
②当![]() 时,因为
时,因为![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上是减函数,又因为
上是减函数,又因为![]() ,所以当
,所以当![]() 时,总有
时,总有![]() ,符合题意.
,符合题意.
③当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,又因为
上是减函数,又因为![]() ,所以当
,所以当![]() 时,总有
时,总有![]() ,不符合题意.
,不符合题意.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b∈R,则“a>0,b>0”是“a+b>0”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
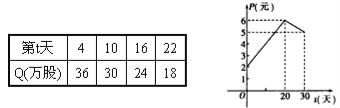
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
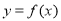 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 平行于同一个平面的两个平面平行
B. 平行于同一直线的两个平面平行
C. 垂直于同一个平面的两条直线平行
D. 垂直于同一条直线的两个平面平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象过点
的图象过点 ,且在点
,且在点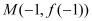 处的切线方程
处的切线方程 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 与
与 的图像有三个交点,求
的图像有三个交点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)是否存在整数
 ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

