【题目】已知二次函数![]() ,关于实数
,关于实数![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式:![]() ;
;
(2)是否存在实数![]() ,使得关于
,使得关于![]() 的函数
的函数![]() 的最小值为-5?若存在,求实数
的最小值为-5?若存在,求实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ,当
,当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
试题分析:(1)借助题设条件运用分类整合思想及二次函数的知识求解;(2)借助题设运用换元法及二次函数的有关知识探求.
试题解析:
(1)由不等式![]() 的解集为
的解集为![]() 知
知
关于![]() 的方程
的方程![]() 的两根为-1和
的两根为-1和![]() ,且
,且![]() ,
,
由根与系数关系,得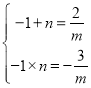 ,∴
,∴![]()
所以原不等式化为![]() ,
,
①当![]() 时,原不等式化为
时,原不等式化为![]() 且
且![]() ,解得
,解得![]() 或
或![]() ;
;
②当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() 且
且![]() ;③
;③
④当![]() 时,原不等式化为
时,原不等式化为![]() 且
且![]() ,解得
,解得![]() 或
或![]() ;
;
综上所述,当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]()
(2)假设存在满足条件的实数![]() ,由(1)得:
,由(1)得:![]() ,
,
![]() ,
,
令![]() ,则
,则![]()
对称轴为![]()
因为![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,解得
,解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段
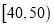 ,
, 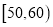 …
…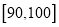 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题: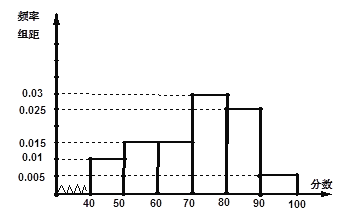
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列
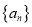 是无穷数列,且各项均为互不相同的正整数,其前
是无穷数列,且各项均为互不相同的正整数,其前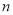 项和为
项和为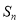 ,数列
,数列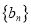 满足
满足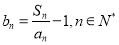 .
.(1)若
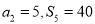 ,求
,求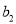 的值;
的值;(2)若数列
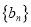 为等差数列,求
为等差数列,求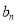 ;
;(3)在(1)的条件下,求证:数列
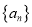 中存在无穷多项(按原来的顺序)成等比数列.
中存在无穷多项(按原来的顺序)成等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
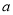 为实数,函数
为实数,函数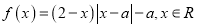 .
.(1)求证:
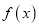 不是
不是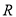 上的奇函数;
上的奇函数;(2)若
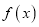 是
是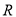 上的单调函数,求实数
上的单调函数,求实数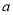 的值;
的值;(3)若函数
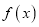 在区间
在区间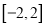 上恰有3个不同的零点,求实数
上恰有3个不同的零点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
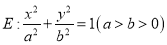 的焦距为
的焦距为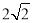 ,其上下顶点分别为
,其上下顶点分别为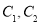 ,点
,点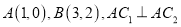 .
.(1)求椭圆
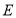 的方程以及离心率;
的方程以及离心率;(2)点
 的坐标为
的坐标为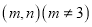 ,过点
,过点 的任意作直线
的任意作直线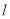 与椭圆
与椭圆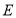 相交于
相交于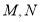 两点,设直线
两点,设直线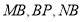 的斜率依次成等差数列,探究
的斜率依次成等差数列,探究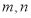 之间是否存在某种数量关系,若是请给出
之间是否存在某种数量关系,若是请给出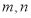 的关系式,并证明;若不是,请说明理由.
的关系式,并证明;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱柱
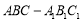 中,
中,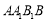 为正方形,
为正方形,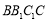 为菱形,
为菱形,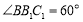 ,平面
,平面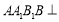 平面
平面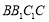 .
.
(1)求证:
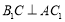 ;
;(2)设点
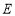 、
、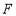 分别是
分别是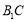 ,
,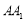 的中点,试判断直线
的中点,试判断直线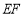 与平面
与平面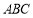 的位置关系,并说明理由;
的位置关系,并说明理由;(3)求二面角
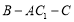 的余弦值.
的余弦值.
相关试题

