【题目】某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如下(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
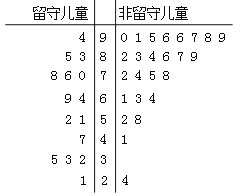
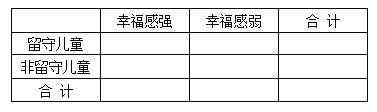
(Ⅰ)根据茎叶图中的数据完成![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为孩子的幸福感强与是否是留守儿童有关?
的把握认为孩子的幸福感强与是否是留守儿童有关?
(Ⅱ)从15个留守儿童中按幸福感强弱进行分层抽样,共抽取5人,又在这5人中随机抽取2人进行家访,求这2个学生中恰有一人幸福感强的概率.
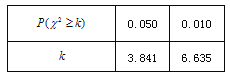
参考公式: 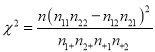 ; 附表:
; 附表:
参考答案:
【答案】(1)有![]() 的把握认为孩子的幸福感强与是否留守儿童有关;(2)
的把握认为孩子的幸福感强与是否留守儿童有关;(2)![]() .
.
【解析】试题分析:(1)由调査数据能作出![]() 列联表,根据观测值的计算公式代入数据做出观测值,把所得的观测值同临界值进行比较,即可得出结论;(2)确定基本事件的个数共有
列联表,根据观测值的计算公式代入数据做出观测值,把所得的观测值同临界值进行比较,即可得出结论;(2)确定基本事件的个数共有![]() 种,这
种,这![]() 个学生中恰有一人幸福感强的事件数共有
个学生中恰有一人幸福感强的事件数共有![]() ,根据古典概型概率公式可得结果.
,根据古典概型概率公式可得结果.
试题解析:(1)列联表如下:
幸福感强 | 幸福感弱 | 总计 | |
留守儿童 | 6 | 9 | 15 |
非留守儿童 | 18 | 7 | 25 |
总计 | 24 | 16 | 40 |
∴![]() .
.
∴有![]() 的把握认为孩子的幸福感强与是否留守儿童有关.
的把握认为孩子的幸福感强与是否留守儿童有关.
(2)按分层抽样的方法可抽出幸福感强的孩子2人,记作: ![]() ,
, ![]() ;幸福感强的孩子3人,记作:
;幸福感强的孩子3人,记作: ![]() ,
, ![]() ,
, ![]() .
.
“抽取2人”包含的基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共10个.
共10个.
事件![]() :“恰有一人幸福感强”包含的基本事件有
:“恰有一人幸福感强”包含的基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共6个.
共6个.
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱
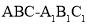 中,
中,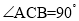 ,
, ,
, 是棱
是棱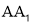 上的一点,
上的一点, 分别为
分别为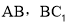 的中点.
的中点.
(1)求证:
 ∥平面
∥平面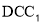 ;
;(2)当
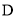 为
为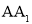 的中点时,求三棱锥
的中点时,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
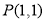 ,过点
,过点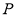 动直线
动直线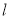 与圆
与圆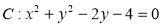 交与点
交与点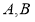 两点.
两点.(1)若
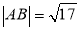 ,求直线
,求直线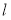 的倾斜角;
的倾斜角;(2)求线段
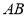 中点
中点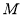 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期
4月1日
4月7日
4月15日
4月21日
4月30日
温差
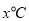
10
11
13
12
8
发芽数
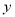 颗
颗23
25
30
26
16
(1)从这5天中任选2天,记发芽的种子数分别为
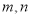 ,求事件“
,求事件“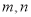 均不小于25”的概率;
均不小于25”的概率;(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出
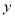 关于
关于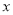 的线性回归方程
的线性回归方程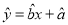 .
.(参考公式:
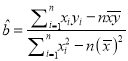 ,
, 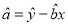 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组:
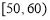 ,
,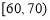 ,
,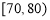 ,
,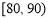 ,
,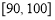 ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在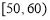 ,
,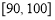 的数据).
的数据).(1)求样本容量
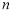 和频率分布直方图中的
和频率分布直方图中的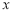 、
、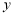 的值;
的值;(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在
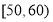 内的概率.
内的概率.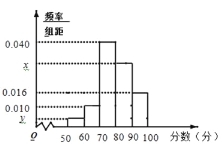

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
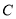 :
: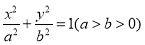 的左、右焦点分别为
的左、右焦点分别为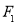 、
、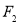 ,左准线
,左准线 :
: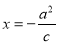 和右准线
和右准线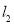 :
: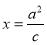 分别与
分别与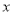 轴相交于
轴相交于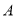 、
、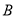 两点,且
两点,且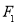 、
、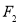 恰好为线段
恰好为线段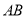 的三等分点.
的三等分点.(1)求椭圆
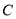 的离心率;
的离心率;(2)过点
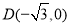 作直线
作直线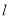 与椭圆相交于
与椭圆相交于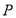 、
、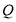 两点,且满足
两点,且满足 ,当△
,当△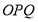 的面积最大时(
的面积最大时(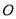 为坐标原点),求椭圆
为坐标原点),求椭圆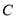 的标准方程.
的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
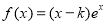 (
(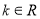 ).
).(1)求
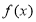 的单调区间和极值;
的单调区间和极值;(2)求
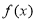 在
在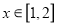 上的最小值.
上的最小值.(3)设
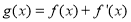 ,若对
,若对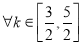 及
及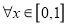 有
有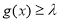 恒成立,求实数
恒成立,求实数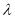 的取值范围.
的取值范围.
相关试题

