
【题目】已知点![]() 是抛物线
是抛物线![]() 的顶点,
的顶点,![]() ,
,![]() 是
是![]() 上的两个动点,且
上的两个动点,且![]() .
.
(1)判断点![]() 是否在直线
是否在直线![]() 上?说明理由;
上?说明理由;
(2)设点![]() 是△
是△![]() 的外接圆的圆心,求点
的外接圆的圆心,求点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析(2)
上,理由见解析(2)![]()
【解析】
(1)由抛物线的方程可得顶点![]() 的坐标,设直线
的坐标,设直线![]() 的方程,与抛物线联立求出两根之和及两根之积,求出数量积
的方程,与抛物线联立求出两根之和及两根之积,求出数量积![]() ,再由题意
,再由题意![]() 可得直线
可得直线![]() 恒过
恒过![]() ,即得
,即得![]() 在直线
在直线![]() 上;
上;
(2)设![]() ,
,![]() 的坐标,可得直线
的坐标,可得直线![]() ,
,![]() 的斜率及线段
的斜率及线段![]() ,
,![]() 的中点坐标,进而求出线段
的中点坐标,进而求出线段![]() ,
,![]() 的中垂线的方程,两个方程联立求出外接圆的圆心
的中垂线的方程,两个方程联立求出外接圆的圆心![]() 的坐标,由(1)可得
的坐标,由(1)可得![]() 的横纵坐标关于参数
的横纵坐标关于参数![]() 的表达式,消参数可得
的表达式,消参数可得![]() 的轨迹方程.
的轨迹方程.
(1) 点![]() 在直线
在直线![]() 上.理由如下,
上.理由如下,
由题意, 抛物线![]() 的顶点为
的顶点为![]()
因为直线与抛物线有2个交点,
所以设直线AB的方程为![]()
联立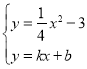 得到
得到![]() ,
,
其中![]() ,
,
![]()
所以![]() ,
,
![]()
![]()
![]()
因为![]()
所以![]()
![]()
![]()
![]()
![]() ,
,
所以![]() ,
,
解得![]() ,
,
经检验,满足![]() ,
,
所以直线AB的方程为![]() ,恒过定点
,恒过定点![]() .
.
(2)因为点![]() 是
是![]() 的外接圆的圆心,所以点
的外接圆的圆心,所以点![]() 是三角形
是三角形![]() 三条边的中垂线的交点,
三条边的中垂线的交点,
设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为为
的中点为为![]() ,
,
因为![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以线段![]() 的中垂线的方程为:
的中垂线的方程为:![]() ,
,
因为![]() 在抛物线上,所以
在抛物线上,所以![]() ,
,
![]() 的中垂线的方程为:
的中垂线的方程为:![]() ,即
,即![]() ,
,
同理可得线段![]() 的中垂线的方程为:
的中垂线的方程为:![]() ,
,
联立两个方程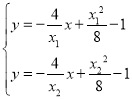 ,解得
,解得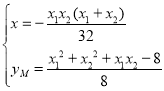 ,
,
由(1)可得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即点![]() ,所以
,所以![]() ,
,
即点![]() 的轨迹方程为:
的轨迹方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数,a∈R).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t为参数,a∈R).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点A(0,4)在直线l上,求直线l的极坐标方程;
(2)已知a>0,若点P在直线l上,点Q在曲线C上,若|PQ|最小值![]() 为,求a的值.
为,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() 焦点在
焦点在![]() 轴上,右顶点
轴上,右顶点![]() 到右焦点的距离与它到右准线的距离之比为
到右焦点的距离与它到右准线的距离之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两点,设
轴对称的任意两点,设![]() ,连接
,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() 并求出点
并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 与曲线
与曲线![]() 、直线
、直线![]() 分别交于
分别交于![]() 、
、![]() 两点(
两点(![]() 异于极点
异于极点![]() ),求
),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
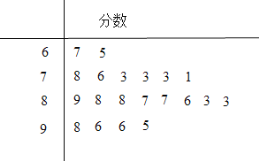
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: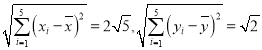
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: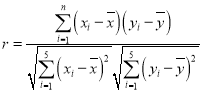 ,
,
参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com