【题目】已知函数![]() ,若
,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则实数
,则实数![]() _______
_______
参考答案:
【答案】![]()
【解析】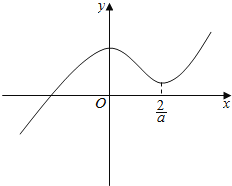
(i)当a=0时,f(x)=3x2+1,令f(x)=0,解得x=±![]() ,函数f(x)有两个零点,舍去。
,函数f(x)有两个零点,舍去。
(ii)当a≠0时,f′(x)=3ax26x=3ax(x![]() ),令f′(x)=0,解得x=0或2a.
),令f′(x)=0,解得x=0或2a.
①当a<0时, ![]() <0,当x<
<0,当x<![]() 或x>0时,f′(x)<0,此时函数f(x)单调递减;当
或x>0时,f′(x)<0,此时函数f(x)单调递减;当![]() <x<0时,f′(x)>0,此时函数f(x)单调递增。
<x<0时,f′(x)>0,此时函数f(x)单调递增。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则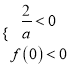 ,无解,舍去。
,无解,舍去。
②当a>0时, ![]() >0,当x>
>0,当x>![]() 或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<
或x<0时,f′(x)>0,此时函数f(x)单调递增;当0<x<![]() 时,f′(x)<0,此时函数f(x)单调递减。
时,f′(x)<0,此时函数f(x)单调递减。
∴![]() 是函数f(x)的极小值点,0是函数f(x)的极大值点。
是函数f(x)的极小值点,0是函数f(x)的极大值点。
∵函数f(x)=ax33x2+1存在唯一的零点x0,且x0<0,则f(![]() >0,即
>0,即![]()
![]() +1>0,a>0,解得a>2.
+1>0,a>0,解得a>2.
综上可得:实数a的取值范围是(2,+∞).
故答案为:(2,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数
10环
9环
8环
7环
概率
0.32
0.28
0.18
0.12
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号
分组
频数
频率
第1组
[50,60)
5
0.05
第2组
[60,70)
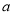
0.35
第3组
[70,80)
30
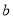
第4组
[80,90)
20
0.20
第5组
[90,100]
10
0.10
合计
100
1.00
(Ⅰ)求
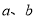 的值;
的值;(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
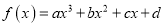 的图象如图所示,则
的图象如图所示,则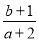 的取值范围是( )
的取值范围是( )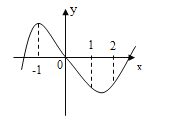
A.
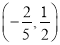 B.
B. 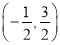 C.
C. 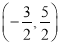 D.
D. 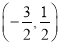
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
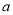 为实数,函数
为实数,函数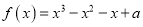 .
.(1)求
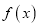 的极值;
的极值;(2)当
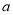 在什么范围内取值时,曲线
在什么范围内取值时,曲线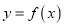 与
与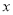 轴仅有一个交点?
轴仅有一个交点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱锥
 的底面为直角梯形,
的底面为直角梯形,  .点
.点 是
是 的中点.
的中点.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)已知平面
 底面
底面 ,且
,且 .在棱
.在棱 上是否存在点
上是否存在点 ,使
,使 ?请说明理由.
?请说明理由.
相关试题

