【题目】《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为![]() ,
,![]() ,且小正方形与大正方形面积之比为
,且小正方形与大正方形面积之比为![]() ,则
,则![]() 的值为( )
的值为( )
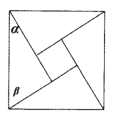
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
设大的正方形的边长为1,由已知可求小正方形的边长,可求cosα﹣sinα=![]() ,sinβ﹣cosβ=
,sinβ﹣cosβ=![]() ,且cosα=sinβ,sinα=cosβ,进而利用两角差的余弦函数公式,同角三角函数基本关系式即可计算得解.
,且cosα=sinβ,sinα=cosβ,进而利用两角差的余弦函数公式,同角三角函数基本关系式即可计算得解.
设大的正方形的边长为1,由于小正方形与大正方形面积之比为9:25,
可得:小正方形的边长为![]() ,
,
可得:cosα﹣sinα=![]() ,①sinβ﹣cosβ=
,①sinβ﹣cosβ=![]() ,②
,②
由图可得:cosα=sinβ,sinα=cosβ,
①×②可得:![]() =cosαsinβ+sinαcosβ﹣cosαcosβ﹣sinαsinβ=sin2β+cos2β﹣cos(α﹣β)=1﹣cos(α﹣β),
=cosαsinβ+sinαcosβ﹣cosαcosβ﹣sinαsinβ=sin2β+cos2β﹣cos(α﹣β)=1﹣cos(α﹣β),
解得:cos(α﹣β)=![]() .
.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是______.
①若直线
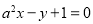 与直线
与直线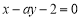 互相垂直,则
互相垂直,则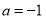
②若
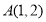 ,
,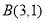 两点到直线
两点到直线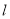 的距离分别是
的距离分别是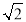 ,
,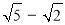 ,则满足条件的直线
,则满足条件的直线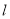 共有3条
共有3条③过
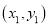 ,
,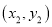 两点的所有直线方程可表示为
两点的所有直线方程可表示为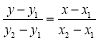
④经过点
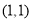 且在
且在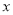 轴和
轴和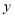 轴上截距都相等的直线方程为
轴上截距都相等的直线方程为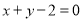
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形
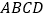 中,
中,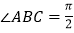 ,
,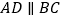 ,
,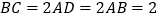 .将梯形
.将梯形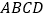 绕
绕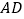 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )
所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A.
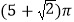 B.
B. 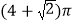 C.
C. 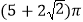 D.
D. 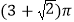
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
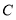 :
: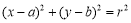 关于直线
关于直线 对称且过点
对称且过点 和
和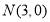 ,直线
,直线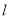 过定点
过定点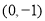 .
.(1)证明:直线
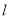 与圆
与圆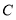 相交;
相交;(2)记直线
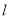 与圆
与圆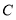 的两个交点为
的两个交点为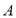 ,
,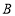 .
.①若弦长
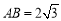 ,求直线方程;
,求直线方程;②求
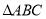 面积的最大值及
面积的最大值及 面积的最大时的直线方程.
面积的最大时的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )
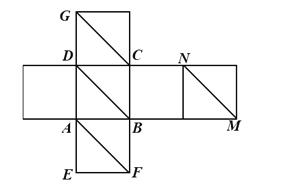
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
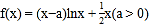 .
.(1)若
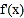 是
是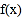 的导函数,讨论
的导函数,讨论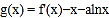 的单调性;
的单调性;(2)若
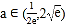 (
(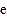 是自然对数的底数),求证:
是自然对数的底数),求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,直线
,直线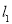 的方程为
的方程为 ,直线
,直线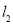 的方程为
的方程为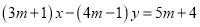 .当m变化时,
.当m变化时,(1)分别求直线
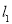 和
和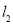 经过的定点坐标;
经过的定点坐标;(2)讨论直线
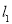 和
和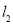 的位置关系.
的位置关系.
相关试题

