【题目】已知函数 ![]() ,
, ![]() , 求解下列问题
, 求解下列问题
(1)求函数 ![]() 的最大值和最小正周期;
的最大值和最小正周期;
(2)设 ![]() 的内角
的内角 ![]() 的对边分别
的对边分别 ![]() 且
且 ![]() ,
, ![]() ,若
,若 ![]() 求
求 ![]() 值.
值.
参考答案:
【答案】
(1)
解: f(x)=![]() sinxcosx-cosx-
sinxcosx-cosx-![]()
=![]() (2sinxcosx)-
(2sinxcosx)-![]() (1+cos2x)-
(1+cos2x)-![]()
=![]() sin2x-
sin2x-![]() cos2x-1
cos2x-1
=sin2xcos![]() -cos2xsin
-cos2xsin![]() -1
-1
=sin(2x-![]() )-1
)-1
故 f(x)的最小正周期是π,最小值是 -2.
(2)
解: f(C)=sin(2C-![]() )-2=-1,
)-2=-1,
∴sin(2C-![]() )=1,
)=1,
∵0<C<π,
∴0<2C<2π,
∴-![]() <2C-
<2C-![]() <
<![]() ,
,
∴2C-![]() =
=![]() ,
,
∴C=![]() .
.
∵sin(A+C)=2sinA,
∴sinB=2sinA,由正弦定理![]() =
=![]() , ①
, ①
∵由余弦定理得:c=a+b-2abcos![]() ,即a+b-ab=9,②
,即a+b-ab=9,②
∴联立①、②解得a=![]() ,b=2
,b=2![]()
【解析】分析:(1)利用两角和与差的三角函数公式及二倍角公式将 ![]() 化成
化成 ![]() 的形式,再根据正弦函数的性质求得.(2)由
的形式,再根据正弦函数的性质求得.(2)由 ![]() ,结合余弦定理得:
,结合余弦定理得: ![]() ;由
;由 ![]() 结合正弦定理得
结合正弦定理得 ![]() ,解方程组可得
,解方程组可得 ![]() 值.
值.
【考点精析】根据题目的已知条件,利用两角和与差的正弦公式和二倍角的正弦公式的相关知识可以得到问题的答案,需要掌握两角和与差的正弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
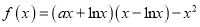 有三个不同的零点
有三个不同的零点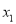 ,
, 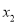 ,
, 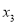 (其中
(其中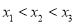 ),则
),则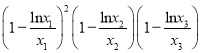 的值为( )
的值为( )A.
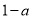 B.
B. 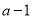 C.
C. 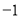 D.
D. 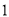
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=


(1)求△ACD的面积;
(2)若BC=2 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的值域为
的值域为 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)是定义在R上的偶函数,在(﹣∞,0]上单调递减,且f(﹣4)=0,则使得x|f(x)+f(﹣x)|<0的x的取值范围是
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的定义域
(1)y=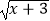 +
+ 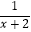
(2)y= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设全集为R,集合A=(﹣∞,﹣1)∪(3,+∞),记函数f(x)=
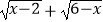 的定义域为集合B
的定义域为集合B
(1)分别求A∩B,A∩RB;
(2)设集合C={x|a+3<x<4a﹣3},若B∩C=C,求实数a的取值范围.
相关试题

