【题目】设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,已知
项和,已知![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() ;
;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)18;(2) ![]()
【解析】试题分析:(1)根据等差数列![]() 满足
满足![]() ,
, ![]() ,列出关于首项
,列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,根据等差数列的求和公式可得
的值,根据等差数列的求和公式可得![]() 递的值;(2)由(1)知
递的值;(2)由(1)知![]() ,从而可得
,从而可得![]() ,利用裂项相消法求解即可.
,利用裂项相消法求解即可.
试题解析:(I)设数列![]() 的公差为
的公差为![]() ,则
,则![]()
即 ![]() ,
,
解得![]() ,
,
所以![]() .
.
(也可利用等差数列的性质解答)
(II)由(I)知![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
【方法点晴】本题主要考查等差数列的通项与求和公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔
 的高度
的高度 (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆 的高度
的高度 米,已知
米,已知 ,
,  .
.(1)该班同学测得
 一组数据:
一组数据:  ,请据此算出
,请据此算出 的值;
的值;(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离
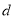 (单位:米),使
(单位:米),使 与
与 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问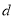 为多大时,
为多大时,  的值最大?
的值最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
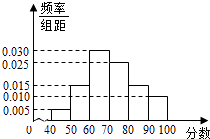
A.588
B.480
C.450
D.120 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题,其中正确的命题序号为( )
①|x+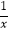 |的最小值是2 ②
|的最小值是2 ② 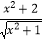 的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2.
的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2.
A.①②③
B.①②④
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】斐波那契数列
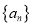 满足:
满足: 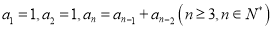 .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前 项所占的格子的面积之和为
项所占的格子的面积之和为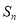 ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为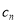 ,则下列结论错误的是( )
,则下列结论错误的是( )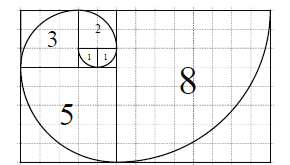
A.
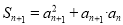 B.
B. 
C.
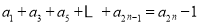 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设圆
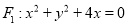 的圆心为
的圆心为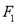 ,直线
,直线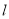 过点
过点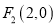 且不与
且不与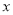 轴、
轴、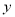 轴垂直,且与圆
轴垂直,且与圆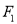 于
于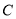 ,
, 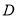 两点,过
两点,过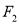 作
作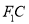 的平行线交直线
的平行线交直线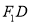 于点
于点 .
.(1)证明
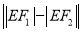 为定值,并写出点
为定值,并写出点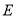 的轨迹方程;
的轨迹方程;(2)设点
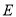 的轨迹为曲线
的轨迹为曲线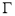 ,直线
,直线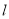 交
交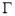 于
于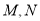 两点,过
两点,过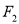 且与
且与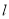 垂直的直线与圆
垂直的直线与圆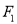 交于
交于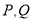 两点,求
两点,求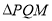 与
与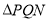 的面积之和的取值范围.
的面积之和的取值范围.
相关试题

