搜索
【题目】如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将三角形ADE沿AE折起，则下列说法正确的是________(填序号)．
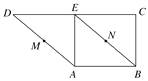
①不论D折至何位置(不在平面ABC内)，都有MN∥平面DEC；②不论D折至何位置，都有MN⊥AE；③不论D折至何位置(不在平面ABC内)，都有MN∥AB；④在折起过程中，一定存在某个位置，使EC⊥AD.
参考答案：
【答案】①②④
【解析】试题分析：将三角形ADE沿AE折起后几何体如图所示：
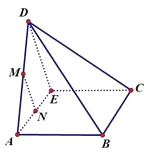
①因为M、N分别是AD、BE的中点，所以不论D折至何位置（不在平面ABC内）都有
，
所以①正确；
②
，所以②正确；
③,
而
与
相交，所以
与
相交，所以③错；
④当
时，因为
平面
,所以存在某个位置，使
，所以④正确；故答案为①②④．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在三棱锥PABC中，不能证明AP⊥BC的条件是( )
A. AP⊥PB，AP⊥PC
B. AP⊥PB，BC⊥PB
C. 平面BPC⊥平面APC，BC⊥PC
D. AP⊥平面PBC
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如果函数f（x）在[a，b]上存在x1 ， x2（a＜x1＜x2＜b）满足
， 
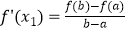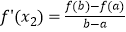，则称函数f（x）是[a，b]上的“双中值函数”．已知函数f（x）=x3﹣x2+a是[0，a]上的“双中值函数”，则实数a的取值范围是（ ）
A.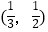
B.（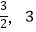
）
C.（
，1）
D.（
，1） -
科目： 来源： 题型：
查看答案和解析>>【题目】设[x]表示不超过x的最大整数，如：[π]=3，[﹣4.3]=﹣5．给出下列命题： ①对任意实数x，都有[x]﹣x≤0；
②若x1≤x2 ， 则[x1]≤[x2]；
③[lg1]+[lg2]+[lg3]+…+[lg100]=90；
④若函数f（x）=
﹣ 
，则y=[f（x）]+[f（﹣x）]的值域为{﹣1，0}．
其中所有真命题的序号是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
E是PC的中点．求证：
（Ⅰ）CD⊥AE；
（Ⅱ）PD⊥平面ABE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知各项均不相等的等差数列{an}的前四项和S4=14，且a1 ， a3 ， a7成等比数列． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）设Tn为数列{
}的前n项和，若Tn≤λan+1对n∈N*恒成立，求实数λ的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，P是四边形ABCD所在平面外的一点，四边形ABCD是∠DAB＝60°且边长为a的菱形．侧面PAD为正三角形，其所在平面垂直于底面ABCD．
（1）若G为AD边的中点，求证：BG⊥平面PAD；
（2）求证：AD⊥PB．
相关试题
