【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
参考答案:
【答案】分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.
【解析】设该企业生产甲产品为![]() 吨,乙产品为
吨,乙产品为![]() 吨,
吨,
该企业可获得利润为![]() ,且
,且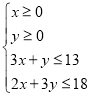 ,(3分)
,(3分)
作出线性约束条件所表示的平面区域如下图中阴影部分所示,
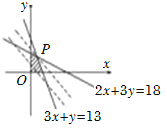 (5分)
(5分)
联立![]() ,解得
,解得![]() ,由图可知,最优解为
,由图可知,最优解为![]() ,(8分)
,(8分)
所以![]() 的最大值为
的最大值为![]() (万元),故在一个生产周期内该企业分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.(10分)
(万元),故在一个生产周期内该企业分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A、B、C的对边分别为a,b,c.角A,B,C成等差数列.
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,
 为前
为前 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则 _________________尺.
_________________尺. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
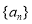 满足
满足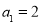 ,
,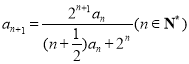 .
.(1)设
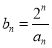 ,求数列
,求数列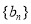 的通项公式;
的通项公式;(2)设
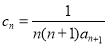 ,求数列
,求数列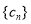 的前n项和为
的前n项和为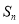 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟)
广告播放时长(分钟)
收视人次(万)
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用
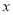 ,
,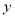 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.(1)用
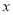 ,
,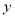 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
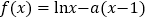
(1)求函数
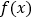 的极值;
的极值;(2)当
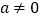 时,过原点分别做曲线
时,过原点分别做曲线 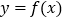 与
与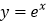 的切线
的切线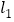 ,
,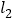 ,若两切线的斜率互为倒数,求证:
,若两切线的斜率互为倒数,求证: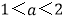 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
相关试题

