【题目】质量监督局检测某种产品的三个质量指标![]() ,用综合指标
,用综合指标![]() 核定该产品的等级.若
核定该产品的等级.若![]() ,则核定该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
,则核定该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 |
|
|
|
|
|
质量指标( |
|
|
|
|
|
产品编号 |
|
|
|
|
|
质量指标( |
|
|
|
|
|
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件![]() 为“在取出的2件产品中,每件产品的综合指标均满足
为“在取出的2件产品中,每件产品的综合指标均满足![]() ”,求事件
”,求事件![]() 的概率.
的概率.
参考答案:
【答案】(1)0.6;(2)![]() .
.
【解析】
(1)分别计算10件产品的综合指标![]() ,找出满足条件
,找出满足条件![]() 的件数,除以总的10件,即可估计总的一等品率;
的件数,除以总的10件,即可估计总的一等品率;
(2)写出所有的基本事件并得其种数,找出满足条件综合指标均有![]() 的基本事件数,由古典概型概率计算公式求得答案.
的基本事件数,由古典概型概率计算公式求得答案.
(1)计算10件产品的综合指标![]() ,如下表:
,如下表:
产品编号 |
|
|
|
|
|
|
|
|
|
|
| 4 | 5 | 6 | 5 | 6 | 5 | 6 | 6 | 3 | 4 |
其中![]() 的有
的有![]() 共6件,故该样本的一等品率为
共6件,故该样本的一等品率为![]() ,
,
从而估计该批产品的一等品率为0.6.
(2)在该样本的一等品中,随机抽取2件产品的所有可能结果为:
![]()
![]() 共15种.
共15种.
在该样本的一等品中,综合指标均满足![]() 的产品编号分别为
的产品编号分别为![]() ,
,
则事件![]() 发生的所有可能结果为
发生的所有可能结果为![]()
![]() 共3种,
共3种,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(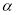 为参数).以
为参数).以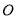 为极点,
为极点,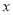 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为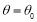 (
(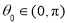 ),将曲线
),将曲线 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线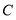 .
.(1)求曲线
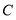 的普通方程和极坐标方程;
的普通方程和极坐标方程;(2)设直线
 与曲线
与曲线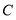 交于
交于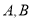 两点,求
两点,求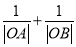 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较两位运动员甲和乙的打靶成绩,在相同条件下测得各打靶
 次所得环数(已按从小到大排列)如下:
次所得环数(已按从小到大排列)如下:甲的环数:
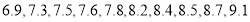
乙的环数:

(1)完成茎叶图,并分别计算两组数据的平均数及方差;

(2)(i)根据(1)的结果,分析两人的成绩;
(ii)如果你是教练,请你作出决策:根据对手实力的强弱分析应该派两人中的哪一位上场比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
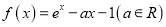 .
.(1)若
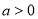 ,试判断
,试判断 的符号;
的符号;(2)讨论
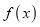 的零点的个数.
的零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值
0~50
51~100
101~150
151~200
201~300

空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占

C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
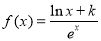 (
(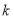 为常数,
为常数,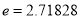 …是自然对数的底数),曲线
…是自然对数的底数),曲线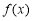 在点
在点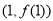 处的切线与
处的切线与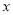 轴平行.
轴平行.(1)求
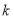 的值;
的值;(2)求函数
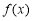 的单调区间;
的单调区间;(3)设
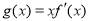 ,其中
,其中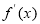 为
为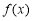 的导函数.证明:对任意
的导函数.证明:对任意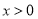 ,
,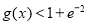 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入
 种黄瓜的年收入
种黄瓜的年收入 与投入
与投入 (单位:万元)满足
(单位:万元)满足 .设甲大棚的投入为
.设甲大棚的投入为 (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为 (单位:万元)
(单位:万元)(1)求
 的值;
的值;(2)试问如何安排甲、乙两个大棚的投入,才能使总收益
 最大?
最大?
相关试题

