【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 |
|
|
|
|
该公司从注册的会员中,随机抽取了![]() 位进行统计,得到统计数据如下:
位进行统计,得到统计数据如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元.根据所给数据,解答下列问题:
元.根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)该公司从至少消费两次的顾客中按消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品.求抽出的2人中恰有1人消费两次的概率.
参考答案:
【答案】(1)![]() ;(2)公司这两次服务的平均利润为
;(2)公司这两次服务的平均利润为![]() 元;(3)抽出的2人中恰有1人消费两次的概率
元;(3)抽出的2人中恰有1人消费两次的概率![]() .
.
【解析】
(1)至少消费两次的会员有40人,根据概率公式![]() ;(2)分别求出两次消费为公司获得的利润,然后求平均值即可;(3) 利用列举法列举出从这8人中抽出2人发放纪念品的事件数,以及求抽出的2人中恰有1人消费两次的事件数,根据古典概型的概率公式求解即可.
;(2)分别求出两次消费为公司获得的利润,然后求平均值即可;(3) 利用列举法列举出从这8人中抽出2人发放纪念品的事件数,以及求抽出的2人中恰有1人消费两次的事件数,根据古典概型的概率公式求解即可.
(1)100位会员中,至少消费两次有40人,
所以估计一位会员至少消费两次的
概率为![]() ;
;
(2)该会员第1次消费时,公司获得利润为![]() (元),
(元),
第2次消费时,公司获得利润为![]() (元),
(元),
所以,公司这两次服务的平均利润为![]() (元);
(元);
(3)至少消费两次的会员中,消费次数分别为2,3,4,5的比例为![]() ,
,
所以抽出的8人中,消费2次的有4人,设为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
消费3次的有2人,设为![]() ,
,![]() ,消费4次和5次的各有1人,分别设为
,消费4次和5次的各有1人,分别设为![]() ,
,![]() ,
,
从中取2人,取到![]() 的有:
的有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共7种;
共7种;
去掉![]() 后,取到
后,取到![]() 的有:
的有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种;
共6种;
去掉![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,取到
后,取到![]() 的有:
的有:![]() 共1种;
共1种;
总的取法有![]() 种,
种,
其中恰有1人消费两次的取法共有:![]() 种,
种,
所以,抽出的2人中恰有1人消费两次的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )

A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥A﹣BCD中,侧棱AB、AC、AD两两垂直,△ABC,△ACD,△ADB的面积分别为
 ,
,  ,
,  , 则三棱锥A﹣BCD的外接球的体积为
, 则三棱锥A﹣BCD的外接球的体积为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,四边形
中,四边形 四边均相等,点
四边均相等,点 在面
在面 的射影为
的射影为 中点
中点 .
.
(1)证明:
 ;
;(2)若
 ,
, ,
, ,求
,求 点到面
点到面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是平行四边形,平面
是平行四边形,平面 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.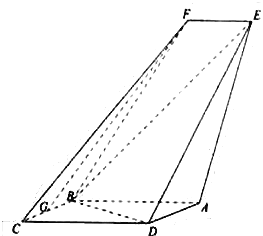
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)已知过原点的动直线
 与圆
与圆
 相交于不同的两点
相交于不同的两点 ,
, .
.(1)求圆
 的圆心坐标;
的圆心坐标;(2)求线段
 的中点
的中点 的轨迹
的轨迹 的方程;
的方程;(3)是否存在实数
 ,使得直线
,使得直线
 与曲线
与曲线 只有一个交点?若存在,求出
只有一个交点?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[0, ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
相关试题

