搜索
【题目】设F1 ， F2是双曲线C： 
（a＞0，b＞0）的两个焦点，P是C上一点，若|PF1|+|PF2|=6a，且△PF1F2的最小内角为30°，则C的离心率为 ．
参考答案：
【答案】
【解析】解：因为F1、F2是双曲线的两个焦点，P是双曲线上一点，且满足|PF1|+|PF2|=6a，
不妨设P是双曲线右支上的一点，由双曲线的定义可知|PF1|﹣|PF2|=2a
所以|F1F2|=2c，|PF1|=4a，|PF2|=2a，
∵△PF1F2的最小内角∠PF1F2=30°，由余弦定理，
∴|PF2|2=|F1F2|2+|PF1|2﹣2|F1F2||PF1|cos∠PF1F2 ，
即4a2=4c2+16a2﹣2×2c×4a× 
，
∴c2﹣2 ca+3a2=0，
∴c= a
所以e= 
= ．
所以答案是： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在等差数列{an}中，2a9＝a12+13，a3＝7，其前n项和为Sn．
（1）求数列{an}的通项公式；
（2）求数列{
}的前n项和Tn，并证明Tn＜
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于
的不等式
.（1）当
时，解不等式；（2）如果不等式的解集为空集，求实数
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】在等腰直角三角形ABC中，AB=AC=4，点P是边AB边上异于AB的一点，光线从点P出发，经BC，CA反射后又回到点P（如图），若光线QR经过△ABC的重心，则AP等于（ ）
A.2
B.1
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】设Sn为数列{an}的前n项和，Sn=（﹣1）nan﹣
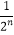，n∈N* ， 则
①a3=；
②S1+S2+…+S100= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】2018年6月14日，世界杯足球赛在俄罗斯拉开帷幕.通过随机调查某小区100名性别不同的居民是否观看世界杯比赛，得到以下列联表：
观看世界杯
不观看世界杯
总计
男
40
20
60
女
15
25
40
总计
55
45
100
经计算
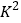的观测值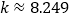
.附表：
0.05
0.025
0.010
0.005
0.001
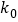
3.841
5.024
6.635
7.879
10.828
参照附表，所得结论正确的是（ ）
A. 有
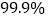以上的把握认为“该小区居民是否观看世界杯与性别有关”B. 有
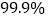以上的把握认为“该小区居民是否观看世界杯与性别无关”C. 在犯错误的概率不超过0.005的前提下，认为“该小区居民是否观看世界杯与性别有关”
D. 在犯错误的概率不超过0.001的前提下，认为“该小区居民是否观看世界杯与性别无关”
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=ax+bx﹣cx ， 其中c＞a＞0，c＞b＞0．
（1）记集合M={（a，b，c）|a，b，c不能构成一个三角形的三条边长，且a=b}，则（a，b，c）∈M所对应的f（x）的零点的取值集合为 ．
（2）若a，b，c是△ABC的三条边长，则下列结论正确的是 ． （写出所有正确结论的序号）
①x∈（﹣∞，1），f（x）＞0；
②x∈R，使ax ， bx ， cx不能构成一个三角形的三条边长；
③若△ABC为钝角三角形，则x∈（1，2），使f（x）=0．
相关试题
