【题目】在极坐标系中,曲线C1:ρsin2θ=4cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C2的参数方程为: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲线C:
]),曲线C:  (t为参数).
(t为参数).
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)C与C1相交于A,B,与C2相切于点Q,求|AQ|﹣|BQ|的值.
参考答案:
【答案】解:(Ⅰ)∵x=ρcosθ,y=ρsinθ, 由ρsin2θ=4cosθ,得ρ2sin2θ=4ρcosθ,
∴曲线C1的直角坐标方程为:y2=4x.
(Ⅱ)设Q(cosθ,sinθ),(θ∈[﹣ ![]() ,
, ![]() ]),由题意知直线C的斜率k=
]),由题意知直线C的斜率k= ![]() ,
,
所以 ![]() ,即
,即 ![]() =tanθ=﹣
=tanθ=﹣ ![]() ,
,
所以 ![]() ,故Q(
,故Q( ![]() ,﹣
,﹣ ![]() ).
).
取 ![]() ,
, ![]() ,不妨设A,B对应的参数分别为t1 , t2 .
,不妨设A,B对应的参数分别为t1 , t2 .
把 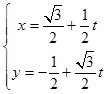 ,代入y2=4x,
,代入y2=4x,
化简得 ![]() ,即3t2﹣(8+2
,即3t2﹣(8+2 ![]() )t﹣8
)t﹣8 ![]() =0,
=0,
∵C与C1相交于A,B,∴△>0,t1+t2= ![]() .
.
∴|AQ|﹣|BQ|=|t1+t2|= ![]()
【解析】(Ⅰ)由x=ρcosθ,y=ρsinθ,能求出曲线C1的直角坐标方程.(Ⅱ)设Q(cosθ,sinθ),(θ∈[﹣ ![]() ,
, ![]() ]),由题意知直线C的斜率k=
]),由题意知直线C的斜率k= ![]() ,从而
,从而 ![]() =tanθ=﹣
=tanθ=﹣ ![]() ,进而Q(
,进而Q( ![]() ,﹣
,﹣ ![]() ).设A,B对应的参数分别为t1 , t2 . 把
).设A,B对应的参数分别为t1 , t2 . 把 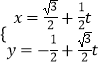 ,代入y2=4x,得3t2﹣(8+2
,代入y2=4x,得3t2﹣(8+2 ![]() )t﹣8
)t﹣8 ![]() =0,由此利用韦达定理能求出|AQ|﹣|BQ|.
=0,由此利用韦达定理能求出|AQ|﹣|BQ|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+y2=16,F(﹣1,0),M是圆C上的一个动点,线段MF的垂直平分线与线段MC相交于点P.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)记点P的轨迹为C1 , A、B是直线x=﹣2上的两点,满足AF⊥BF,曲线C1与过A,B的两条切线(异于x=﹣2)交于点Q,求四边形AQBF面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=xln(ax+1)(a≠0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若a>0且满足:对x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤ln3﹣ln2,试比较ea﹣1与 的大小,并证明.
的大小,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】曲线
 是平面内到定点
是平面内到定点 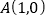 的距离与到定直线
的距离与到定直线  的距离之和为
的距离之和为  的动点
的动点  的轨迹.则曲线
的轨迹.则曲线  与
与 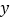 轴交点的坐标是________________;又已知点
轴交点的坐标是________________;又已知点  (
(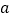 为常数),那么
为常数),那么 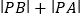 的最小值
的最小值  ________________.
________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家秦九韶(约公元1202﹣1261年)给出了求n(n∈N*)次多项式anxn+an﹣1xn﹣1+…+a1x+a0 , 当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0 , 然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.

A.x4+x3+2x2+3x+4
B.x4+2x3+3x2+4x+5
C.x3+x2+2x+3
D.x3+2x2+3x+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

 过点
过点  ,且与
,且与  的交于
的交于  ,
,  .
.(1) 用
 表示
表示  ,
,  的横坐标;
的横坐标;(2)设以
 为焦点,过点
为焦点,过点  ,
,  且开口向左的抛物线的顶点坐标为
且开口向左的抛物线的顶点坐标为  ,求实数
,求实数 
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X<μ+2σ)=0.954 4,P(μ-σ<X<μ+σ)=0.682 6.若μ=4,σ=1,则P(5<X<6)=( )
A. 0.135 9 B. 0.135 8 C. 0.271 8 D. 0.271 6;
相关试题

