【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
参考答案:
【答案】D
【解析】解:A.函数的周期为2kπ,当k=﹣1时,周期T=﹣2π,故A正确,
B.当x= ![]() 时,cos(x+
时,cos(x+ ![]() )=cos(
)=cos( ![]() +
+ ![]() )=cos
)=cos ![]() =cos3π=﹣1为最小值,此时y=f(x)的图象关于直线x=
=cos3π=﹣1为最小值,此时y=f(x)的图象关于直线x= ![]() 对称,故B正确,
对称,故B正确,
C当x= ![]() 时,f(
时,f( ![]() +π)=cos(
+π)=cos( ![]() +π+
+π+ ![]() )=cos
)=cos ![]() =0,则f(x+π)的一个零点为x=
=0,则f(x+π)的一个零点为x= ![]() ,故C正确,
,故C正确,
D.当 ![]() <x<π时,
<x<π时, ![]() <x+
<x+ ![]() <
< ![]() ,此时余弦函数不是单调函数,故D错误,
,此时余弦函数不是单调函数,故D错误,
故选:D
【考点精析】掌握余弦函数的单调性和余弦函数的对称性是解答本题的根本,需要知道余弦函数的单调性:在![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;余弦函数的对称性:对称中心
上是减函数;余弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查
 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种 ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:班号
一班
二班
三班
四班
五班
六班
频数
5
9
11
9
7
9
满意人数
4
7
8
5
6
6
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为
 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cosx,C2:y=sin(2x+
 ),则下面结论正确的是( )
),则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移  个单位长度,得到曲线C2
个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移  个单位长度,得到曲线C2
个单位长度,得到曲线C2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若
 =λ
=λ  +μ
+μ  ,则λ+μ的最大值为( )
,则λ+μ的最大值为( )
A.3
B.2
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
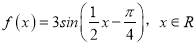 .
.(1)利用“五点法”画出函数
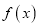 在一个周期
在一个周期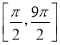 上的简图;
上的简图;(2)先把
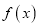 的图象上所有点向左平移
的图象上所有点向左平移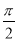 个单位长度,得到
个单位长度,得到 的图象;然后把
的图象;然后把 的图
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到
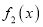 的图象;再把
的图象;再把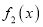 的图象
的图象上所有点的纵坐标缩短到原来的
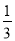 倍(横坐标不变),得到
倍(横坐标不变),得到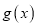 的图象,求
的图象,求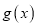 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=60°,AB=3,AC=2.若
 =2
=2  ,
,  =λ
=λ  ﹣
﹣  (λ∈R),且
(λ∈R),且  =﹣4,则λ的值为 .
=﹣4,则λ的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的参数方程是
的参数方程是 为参数
为参数 ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 .
.(1)写出
 的极坐标方程和
的极坐标方程和 的直角坐标方程;
的直角坐标方程;(2)已知点
 、
、 的极坐标分别是
的极坐标分别是 、
、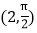 ,直线
,直线 与曲线
与曲线 相交于P、Q两点,射线OP与曲线
相交于P、Q两点,射线OP与曲线 相交于点A,射线OQ与曲线
相交于点A,射线OQ与曲线 相交于点B,求
相交于点B,求 的值.
的值.
相关试题

