【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(log4a)+f(lo ![]() a)≤2f(1),则实数a的取值范围是 .
a)≤2f(1),则实数a的取值范围是 .
参考答案:
【答案】[ ![]() ,4]
,4]
【解析】解:由于函数f(x)是定义在R上的偶函数, 则f(﹣x)=f(x),即有f(x)=f(|x|),
由实数a满足f(log4a)+f(lo ![]() a)≤2f(1),
a)≤2f(1),
则有f(log4a)+f(﹣log4a)≤2f(1),
即2f(log4a)≤2f(1)即f(log4a)≤f(1),
即有f(|log4a|)≤f(1),
由于f(x)在区间[0,+∞)上单调递增,
则|log4a|≤1,即有﹣1≤log4a≤1,
解得, ![]() ≤a≤4.
≤a≤4.
所以答案是:[ ![]() ,4].
,4].
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等比数列,且满足a2+a5=36,a3a4=128. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}是递增数列,且bn=an+log2an(n∈N*),求数列{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断:
①从个体编号为1,2,…,1000的总体中抽取一个容量为50的样本,若采用系统抽样方法进行抽取,则分段间隔应为20;
②已知某种彩票的中奖概率为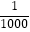 ,那么买1000张这种彩票就一定会中奖(假设该彩票有足够的张数);
,那么买1000张这种彩票就一定会中奖(假设该彩票有足够的张数);
③从装有2个红球和2个黒球的口袋内任取2个球,恰有1个黒球与恰有2个黒球是互斥但不对立的两个事件;
④设具有线性相关关系的变量的一组数据是(1,3),(2,5),(3,6),(6,8),则它们的回归直线一定过点(3,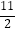 ).
).
其中正确的序号是( )
A.①、②、③
B.①、③、④
C.③、④
D.①、③ -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式ax2+bx+c>0的解集为{x|﹣1<x<2},则不等式a(x2+1)+b(x﹣1)+c>2ax的解集为( )
A.{x|0<x<3}
B.{x|x<0或x>3}
C.{x|﹣2<x<1}
D.{x|x<﹣2或x>1} -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
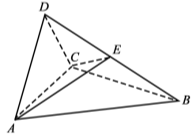
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8. (Ⅰ)若a=2,b=
 ,求cosC的值;
,求cosC的值;
(Ⅱ)若sinAcos2 +sinBcos2
+sinBcos2  =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=  sinC,求a和b的值.
sinC,求a和b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}是等差数列,若
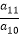 <﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
<﹣1,且它的前n项和Sn有最大值,那么当Sn取的最小正值时,n=( )
A.11
B.17
C.19
D.21
相关试题

