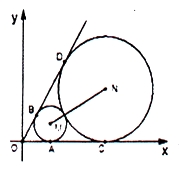
【题目】如图,已知圆心坐标为![]() 的圆
的圆![]() 与
与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点,另一圆
两点,另一圆![]() 与圆
与圆![]() 外切,且与
外切,且与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点.
两点.
(1)求圆![]() 和圆
和圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 的平行线
的平行线![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得的弦的长度.
截得的弦的长度.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)圆![]() 的圆心已知,且其与
的圆心已知,且其与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 两点,故半径易知,另一圆
两点,故半径易知,另一圆![]() 与圆
与圆![]() 外切、且与
外切、且与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)由于
两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)由于![]() 点位置不特殊,可以由对称性转化为求过
点位置不特殊,可以由对称性转化为求过![]() 点且与线
点且与线![]() 平行的线被圆截得弦的长度.
平行的线被圆截得弦的长度.
试题解析:(1)由于![]() 与
与![]() 的两边均相切,故
的两边均相切,故![]() 到
到![]() 及
及![]() 的距离均为
的距离均为![]() 的半径,则
的半径,则![]() 在
在![]() 的平分线上,同理,
的平分线上,同理,![]() 也
也![]() 在的平分线上,
在的平分线上,
即![]() 三点共线,且
三点共线,且![]() 为
为![]() 的平分线,
的平分线,
∵![]() 的坐标为
的坐标为![]() ,∴
,∴![]() 到
到![]() 轴的距离为1,即
轴的距离为1,即![]() 的半径为1,
的半径为1,
则![]() 的方程为
的方程为![]() ,
,
设![]() 的半径为
的半径为![]() ,其与
,其与![]() 轴的切点为
轴的切点为![]() ,连接
,连接![]() 、
、![]() ,
,
由![]() 可知,
可知,![]() ,
,
即![]() .
.
则![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ;
;
(2)由对称性可知,所求的弦长等于过![]() 点,直线
点,直线![]() 的平行线被圆
的平行线被圆![]() 截得的弦的长度,
截得的弦的长度,
此弦的方程是![]() ,即:
,即:![]() ,
,
圆心![]() 到该直线的距离
到该直线的距离![]() ,则弦长=
,则弦长=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.(Ⅰ)求实数
 的值;
的值;(Ⅱ)若函数
 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;(Ⅲ)设
 是函数
是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的一点与平面外的一点的连线与这个平面内的直线的关系是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,已知直线
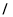 过点
过点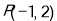 ,倾斜角
,倾斜角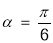 ,再以原点为极点,
,再以原点为极点,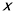 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为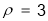 .
.(1)写出直线
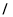 的参数方程和曲线
的参数方程和曲线 的直角坐标方程;
的直角坐标方程;(2)若直线
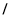 与曲线
与曲线 分别交于
分别交于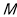 、
、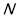 两点,求
两点,求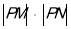 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.

(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且
 ,求∠BAC.
,求∠BAC.
相关试题

