【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:![]() .
.
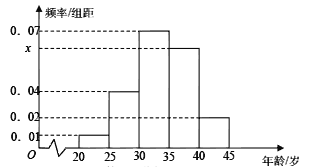
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() 人;(Ⅱ)
人;(Ⅱ)![]() 的分布列见解析,
的分布列见解析,![]() .
.
【解析】
试题分析:(Ⅰ)小矩形的面积等于频率,故![]() ,年龄在
,年龄在![]() 岁的人数为
岁的人数为![]() (人);(Ⅱ)
(人);(Ⅱ)![]() 的可能取值为
的可能取值为![]() ,依题计算各变量对应概率,列出分布列,计算均值.
,依题计算各变量对应概率,列出分布列,计算均值.
试题解析:(Ⅰ)∵小矩形的面积等于频率,∴除![]() 外的频率和为
外的频率和为![]() ,
,
∴![]()
500名志愿者中,年龄在![]() 岁的人数为
岁的人数为![]() (人)
(人)
(Ⅱ)用分层抽样的方法,从中选取10名,则其中年龄“低于35岁”的人有6名,“年龄不低于35岁”的人有4名,故![]() 的可能取值为
的可能取值为![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
故![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过抛物线
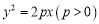 上一点
上一点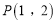 ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于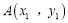 ,
,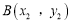 ,当
,当 与
与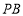 的斜率存在且倾斜角互补时:
的斜率存在且倾斜角互补时: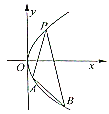
(Ⅰ)求
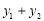 的值;
的值;(Ⅱ)若直线
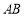 在
在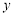 轴上的截距
轴上的截距 时,求
时,求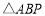 面积
面积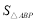 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
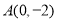 ,椭圆
,椭圆 :
: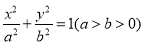 的离心率为
的离心率为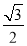 ,
,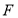 是椭圆的焦点,直线
是椭圆的焦点,直线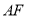 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.(Ⅰ)求
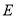 的方程;
的方程;(Ⅱ)设过点
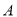 的直线
的直线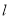 与
与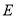 相交于
相交于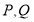 两点,当
两点,当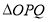 的面积最大时,求
的面积最大时,求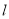 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数,得到如下数据:
日期
12月1日
12月2日
12月3日
12月4日
12月5日
温差
 (℃)
(℃)10
11
13
12
8
发芽数
 (颗)
(颗)23
25
30
26
16
该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是不相邻的2天数据的概率;
(Ⅱ)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求
 关于
关于 的线性回归方程
的线性回归方程 ;
;(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅱ)中所得的线性回归方程是否可靠?
(注:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图(图1)和频率分布直方图(图2)都受到不同程度的破坏,可见部分如图所示,据此解答如下问题.
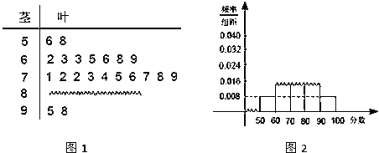
(1)求该集训队总人数及分数在[80,90)之间的频数;
(2)计算频率分布直方图中[80,90)的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生的答题情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
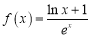 (
(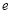 是自然对数的底数),
是自然对数的底数),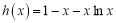 .
.(Ⅰ)求曲线
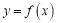 在点
在点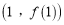 处的切线方程;
处的切线方程;(Ⅱ)求
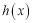 的最大值;
的最大值;(Ⅲ)设
 ,其中
,其中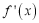 为
为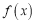 的导函数,证明:对任意
的导函数,证明:对任意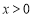 ,
,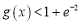 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以
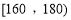 ,
, ,
,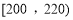 ,
,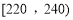 ,
, ,
,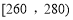 ,
,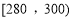 分组的频率分布直方图如图:
分组的频率分布直方图如图: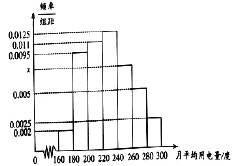
(Ⅰ)求直方图中
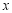 的值;
的值;(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为
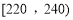 ,
, ,
,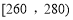 ,
,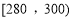 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在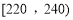 的用户中应抽取多少户?
的用户中应抽取多少户?
相关试题

