【题目】设函数f(x)=(x+a)lnx,g(x)= ![]() ,已知曲线y=f(x)在x=1处的切线过点(2,3).
,已知曲线y=f(x)在x=1处的切线过点(2,3).
(1)求实数a的值.
(2)是否存在自然数k,使得函数y=f(x)﹣g(x)在(k,k+1)内存在唯一的零点?如果存在,求出k;如果不存在,请说明理由.
(3)设函数h(x)=min{f(x),g(x)},(其中min{p,q}表示p,q中的较小值),对于实数m,x0∈(0,+∞),使得h(x0)≥m成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:由f(x)=(x+a)lnx,得f′(x)=lnx+ ![]() ,
,
则f'(1)=a+1,f(1)=0,
∴f(x)在x=1处的切线方程为y=(1+a)(x﹣1),代入(2,3),得3=1+a,即a=2
(2)解:存在k=1符合题意,证明如下:
令 ![]() ,
,
当x∈(0,1]时,φ(x)<0,φ(2)= ![]() >
> ![]() ,
,
∴φ(1)φ(2)<0.
可得x0∈(1,2),使得φ(x0)=0,
φ′(x)=lnx+ ![]() +
+ ![]() ,
,
当x∈(1,2)时,φ′(x)>1+ ![]()
![]() >0;
>0;
当x∈[2,+∞)时,φ′(x)=lnx+ ![]() +
+ ![]() >0.
>0.
即x∈(1,+∞)时,φ′(x)>0.
φ(x)在(1,+∞)上单调递增.
可得φ(x)=0在(1,2)有唯一实根.
∴存在k=1使得函数y=f(x)﹣g(x)在(k,k+1)内存在唯一的零点
(3)解:x0∈(0,+∞),使得h(x0)≥m成立,则m≤hmax(x).
由(2)知,函数y=f(x)﹣g(x)在(k,k+1)内存在唯一的零点x0 .
当x∈(0,x0)时,f(x)<g(x),x∈(x0,+∞)时,f(x)>g(x),
∴h(x)= 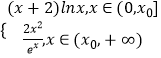 ,
,
当x∈(0,x0]时,若x∈(0,1],h(x)=f(x)≤0,
若x∈(1,x0],h′(x)=lnx+ ![]() >0,h(x)在(1,x0]上单调递增,
>0,h(x)在(1,x0]上单调递增,
∴0<h(x)≤h(x0),
当x∈(x0,+∞)时,h′(x)= ![]() ,
,
可得x∈(x0,2)时,h′(x)>0,h(x)单调递增,x∈(2,+∞)时,h′(x)<0,h(x)单调递减.
∴x∈(x0,+∞)时,h(x)≤h(2)= ![]() ,且h(x0)<h(2).
,且h(x0)<h(2).
可得 ![]() .
.
∴ ![]() 时,x0∈(0,+∞),使得h(x0)≥m成立
时,x0∈(0,+∞),使得h(x0)≥m成立
【解析】(1)利用导数求出函数f(x)在x=1处的切线方程,把点(2,3)代入切线方程即可求得实数a的值;(2)构造函数 ![]() ,利用导数判断x∈(1,+∞)时,φ′(x)>0,φ(x)在(1,+∞)上单调递增.结合φ(1)φ(2)<0,可得x0∈(1,2),使得φ(x0)=0,从而求得k值;(3)由题意写出分段函数h(x),然后利用导数分类求出函数的最大值,得到h(x)在(0,+∞)上的最大值,即可求得满足条件的实数m的取值范围.
,利用导数判断x∈(1,+∞)时,φ′(x)>0,φ(x)在(1,+∞)上单调递增.结合φ(1)φ(2)<0,可得x0∈(1,2),使得φ(x0)=0,从而求得k值;(3)由题意写出分段函数h(x),然后利用导数分类求出函数的最大值,得到h(x)在(0,+∞)上的最大值,即可求得满足条件的实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经研究发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:f(t)=
 ,
,
(1)求出k的值,并指出讲课开始后多少分钟,学生的注意力最集中?能坚持多久?
(2)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到185,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.

(1)求证:AM∥平面PCD;
(2)设点N是线段CD上的一动点,当点N在何处时,直线MN与平面PAB所成的角最大?并求出最大角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生更多的了解“数学史”知识,梁才学校高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号
分组
组中值
频数
频率
(i)
(分数)
(Gi)
(人数)
(Fi)
1

65
①
0.12
2

75
20
②
3

85
③
0.24
4

95
④
⑤
合计
50
1
(1)填充频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在
参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程为
 ,(t为参数),以坐标原点为极点,x正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=
,(t为参数),以坐标原点为极点,x正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=  .
.
(1)写出直线l的极坐标方程与曲线C的直角坐标方程.
(2)若点P是曲线C上的动点,求点P到直线l的距离的最小值,并求出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.

(1)根据散点图判断,在推广期内,
 与
与 (
( ,
, 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次 关于活动推出天数
关于活动推出天数 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);(2)若y关于x的回归方程不是线性的可通过换元方法把它化归为线性回归方程。例如:
 (a、b为常数,e为自然对数的底数),可以两边同时取自然对数
(a、b为常数,e为自然对数的底数),可以两边同时取自然对数 ,再令
,再令 ,先用最小二乘法求出
,先用最小二乘法求出 与x的线性回归方程,再得出y与x的回归方程。根据(1)的判断结果及表1中的数据,求y关于x的回归方程;
与x的线性回归方程,再得出y与x的回归方程。根据(1)的判断结果及表1中的数据,求y关于x的回归方程;(3)由(2)中的归方程预测活动推出第12天使用扫码支付的人次。
参考数据:





66
1.54
2711
50.12
3.47
其中
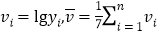 ,参考公式:对于一组数据
,参考公式:对于一组数据 ,
, ,…,
,…, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 ,
, 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x﹣a|,a<0.
(1)证明f(x)+f(﹣ )≥2;
)≥2;
(2)若不等式f(x)+f(2x)< 的解集非空,求a的取值范围.
的解集非空,求a的取值范围.
相关试题

