【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形,已知
是等边三角形,已知![]() ,
,![]() .
.

(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)证得AD⊥BD,而面PAD⊥面ABCD,∴BD⊥面PAD,∴面MBD⊥面PAD.
(2)作辅助线PO⊥AD,则PO为四棱锥P—ABCD的高,求得S四边形ABCD=24.∴VP—ABCD=16![]() .
.
试题解析:
(1)证明:在△ABD中,∵AD=4,BD=8,AB=4![]() ,∴AD2+BD2=AB2.∴AD⊥BD.
,∴AD2+BD2=AB2.∴AD⊥BD.
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,BD面ABCD,∴BD⊥面PAD.
又BD面BDM,∴面MBD⊥面PAD.
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,∴PO⊥面ABCD,即PO为四棱锥P—ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=2![]() .
.
在底面四边形ABCD中,AB∥DC,AB=2DC,∴四边形ABCD为梯形.
在Rt△ADB中,斜边AB边上的高为![]() =
=![]() ,此即为梯形的高.
,此即为梯形的高.
∴S四边形ABCD=![]() ×
×![]() =24.
=24.
∴VP—ABCD=![]() ×24×2
×24×2![]() =16
=16![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤
 )的部分图象,其图象与y轴交于点(0,
)的部分图象,其图象与y轴交于点(0,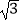 )
)
(Ⅰ)求函数的解析式;
(Ⅱ)若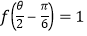 , 求
, 求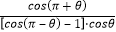 -
-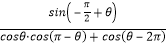 的值.
的值.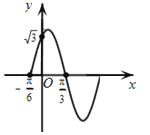
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(1)求证:平面ABC1⊥平面A1ACC1;
(2)设D是线段BB1的中点,求三棱锥D﹣ABC1的体积.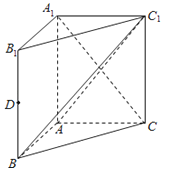
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
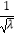 .
.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.F,G是曲线D上不同的两点,对于定点Q(﹣3,0),有|QF||QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强市民的环保意识,某市面向全市增招环保知识义务宣传志愿者,从符合条件的志愿者中随机选取
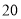 名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第
名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第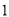 组
组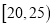 ,第
,第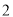 组
组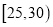 ,第
,第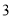 组
组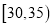 ,第
,第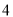 组
组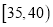 ,第
,第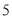 组
组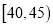 ,得到的频率分布直方图(局部)如图所示.
,得到的频率分布直方图(局部)如图所示.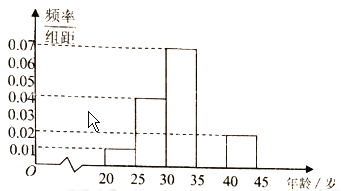
(1)求第
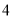 组的频率,并在图中补画直方图;
组的频率,并在图中补画直方图;(2)从
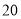 名志愿者中再选出年龄低于
名志愿者中再选出年龄低于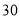 岁的志愿者
岁的志愿者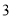 名担任主要宣讲人,求这
名担任主要宣讲人,求这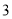 名主要宣讲人的年龄在不同一组的概率.
名主要宣讲人的年龄在不同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
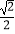 (cosx﹣sinx)sin(x+
(cosx﹣sinx)sin(x+ )﹣2asinx+b(a>0).
)﹣2asinx+b(a>0).
(1)若b=1,且对任意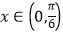 , 恒有f(x)>0,求a的取值范围;
, 恒有f(x)>0,求a的取值范围;
(2)若f(x)的最大值为1,最小值为﹣4,求实数a,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将圆
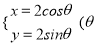 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的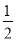 倍,得到曲线
倍,得到曲线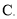
(1)求出
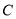 的普通方程;
的普通方程;(2)设直线
 :
: 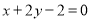 与
与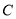 的交点为
的交点为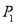 ,
, 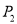 ,以坐标原点为极点,
,以坐标原点为极点, 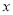 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段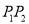 的中点且与
的中点且与 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
相关试题

