【题目】在边长为4的菱形![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() ,连接
,连接![]() ,得到如图所示的五棱锥,且
,得到如图所示的五棱锥,且![]() .
.
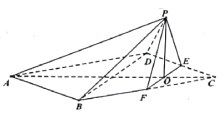
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据菱形性质得![]() ,再根据翻折关系得
,再根据翻折关系得![]() ,结合线面垂直判定定理得
,结合线面垂直判定定理得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论,(2)分别延长
,最后根据面面垂直判定定理得结论,(2)分别延长![]() 和
和![]() 相交于点
相交于点![]() ,过点
,过点![]() 做
做![]() ,根据计算得
,根据计算得![]() ,即得
,即得![]() 平面
平面![]() ,利用三垂线定理及其逆定理证得
,利用三垂线定理及其逆定理证得![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角.最后解直角三角形得二面角的余弦值.
所成二面角的平面角.最后解直角三角形得二面角的余弦值.
试题解析:(1)因为点![]() 分别是边
分别是边![]() 的中点,所有
的中点,所有![]() ,
,
因为菱形![]() 的对角线互相垂直,所以
的对角线互相垂直,所以![]() ,故
,故![]() .
.
翻折后即有![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
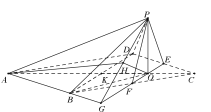
(2)分别延长![]() 和
和![]() 相交于点
相交于点![]() ,连
,连![]() ,设
,设![]() ,连接
,连接![]() ,∵
,∵![]()
∴![]() 为等边三角形.∴
为等边三角形.∴![]() ,
,![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ∴
∴![]() 平面
平面![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
过点![]() 做
做![]() ,连
,连![]() ,则
,则![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角.
所成二面角的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,且
,且 ,若以
,若以 为左右焦点的椭圆
为左右焦点的椭圆 经过点
经过点 .
.(1)求
 的标准方程;
的标准方程;(2)设过
 右焦点且斜率为
右焦点且斜率为 的动直线与
的动直线与 相交于
相交于 两点,探究在
两点,探究在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得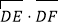 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为常数).
为常数).(1)求函数
 在
在 的最小值;
的最小值;(2)设
 是函数
是函数 的两个零点,且
的两个零点,且 ,证明:
,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,直线
 的参数方程为
的参数方程为 ,(
,( 为参数).以原点为极点,
为参数).以原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;(2)已知与直线
 平行的直线
平行的直线 过点
过点 ,且与曲线
,且与曲线 交于
交于 两点,试求
两点,试求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一200名学生的期中考试语文成绩服从正态分布
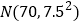 ,数学成绩的频数分布直方图如下:
,数学成绩的频数分布直方图如下:
(1)计算这次考试的数学平均分,并比较语文和数学哪科的平均分较高(假设数学成绩在频率分布直方图中各段是均匀分布的);
(2)如果成绩大于85分的学生为优秀,这200名学生中本次考试语文、数学优秀的人数大约各多少人?
(3)如果语文和数学两科都优秀的共有4人,从(2)中的这些同学中随机抽取3人,设三人中两科都优秀的有
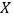 人,求
人,求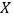 的分布列和数学期望.
的分布列和数学期望.(附参考公式)若
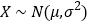 ,则
,则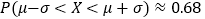 ,
,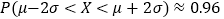
-
科目: 来源: 题型:
查看答案和解析>>【题目】在北上广深等十余大中城市,一款叫“一度用车”的共享汽车给市民们提供了一种新型的出行方式.2020年,怀化也将出现共享汽车,用户每次租车时按行驶里程(1元/公里)加用车时间(0.1元/分钟)收费,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟)
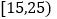
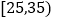
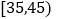
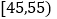
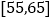
次数
8
14
8
8
2
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为
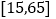 分钟.
分钟.(Ⅰ)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设
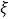 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求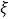 的分布列和期望;
的分布列和期望;(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
-
科目: 来源: 题型:
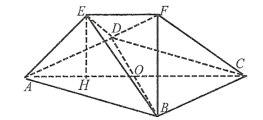
查看答案和解析>>【题目】在如图所示的多面体
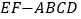 中,底面四边形
中,底面四边形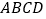 是菱形,
是菱形,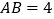 ,
,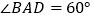 ,
,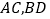 相交于
相交于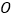 ,
,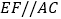 ,
,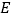 在平面
在平面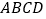 上的射影恰好是线段
上的射影恰好是线段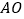 的中点
的中点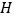 .
.
(Ⅰ)求证:
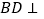 平面
平面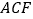 ;
;(Ⅱ)若直线
 与平面
与平面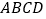 所成的角为
所成的角为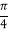 ,求平面
,求平面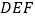 与平面
与平面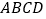 所成锐二面角的余弦值.
所成锐二面角的余弦值.
相关试题

