【题目】(必须列式,不能只写答案,答案用数字表示)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)求共有多少种放法;
(2)求恰有一个盒子不放球,有多少种放法;
(3)求恰有两个盒内不放球,有多少种放法;
参考答案:
【答案】(1)256 (2)144 (3)84
【解析】
试题分析:(1)直接利用分步计数原理求解即可;(2)“恰有一个盒内放2球”与“恰有一个盒子不放球”是一回事,通过小球分组然后求解即可;(3)四个不同的球全部放入4个不同的盒子内,恰有两个盒子不放球的不同放法的求法,分为两步来求解,先把四个球分为两组,再取两个盒子,作全排列,由于四个球分两组有两种分法,一种是2,2,另一种是3,1,故此题分为两类来求解,再求出它们的和
试题解析:(1)一个球一个球地放到盒子里去,每只球都可有4种独立的放法,由分步乘法计数原理,放法共有:44=256种.
(2)“恰有一个盒内放2球”与“恰有一个盒子不放球”是一回事.
选择一个盒子放2个球,有![]() ,选择2个盒子各放一个球的方法数:
,选择2个盒子各放一个球的方法数:![]() ,
,
共有方法数:![]() =144种放法.
=144种放法.
(3)四个球分为两组有两种分法,(2,2),(3,1)
若两组每组有两个球,不同的分法有![]() =3种,恰有两个盒子不放球的不同放法是3×
=3种,恰有两个盒子不放球的不同放法是3×![]() =36种,
=36种,
若两组一组为3,一组为1个球,不同分法有![]() =4种恰有两个盒子不放球的不同放法是4×
=4种恰有两个盒子不放球的不同放法是4×![]() =48种,
=48种,
综上恰有两个盒子不放球的不同放法是36+48=84种
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
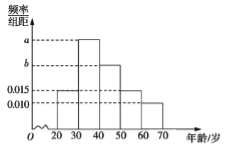
(1)已知中间三个年龄段的网上购票人数成等差数列,求
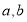 的值;
的值;(2)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:
年龄在
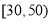 岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】语文成绩服从正态分布
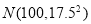 ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
(I)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(II)如果语文和数学两科都特别优秀的共有6人,从(I)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有
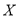 人,求
人,求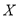 的分布列和数学期望.
的分布列和数学期望.(附参考公式)若
 ,则
,则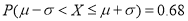 ,
,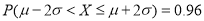 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产甲,乙两种产品均需用
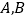 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用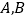 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.甲
乙
原料限额
A(吨)
3
2
12
B(吨)
1
2
8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
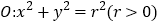 与直线
与直线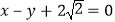 相切.
相切.(1)求圆
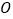 的方程;
的方程;(2)过点
 的直线
的直线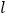 截圆
截圆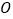 所得弦长为
所得弦长为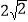 ,求直线
,求直线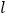 的方程;
的方程;(3)设圆
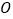 与
与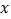 轴的负半抽的交点为
轴的负半抽的交点为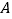 ,过点
,过点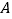 作两条斜率分别为
作两条斜率分别为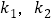 的直线交圆
的直线交圆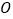 于
于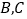 两点,且
两点,且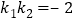 ,证明:直线
,证明:直线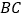 过定点,并求出该定点坐标.
过定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
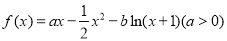 ,
,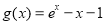 ,曲线
,曲线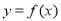 与
与 在原点处有公共切线.
在原点处有公共切线.(I)若
 为函数的极大值点,求
为函数的极大值点,求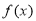 的单调区间(用
的单调区间(用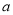 表示);
表示);(II)若
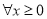 ,
,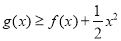 ,求
,求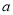 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
相关试题

