【题目】已知数列{an}满足a1=1,a2=2,an+2=(1+cos2 ![]() )an+sin2
)an+sin2 ![]() ,则该数列的前10项和为 .
,则该数列的前10项和为 .
参考答案:
【答案】77
【解析】解:因为a1=1,a2=2,所以a3=(1+cos2 ![]() )a1+sin2
)a1+sin2 ![]() =a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.
=a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.
一般地,当n=2k﹣1(k∈N*)时,a2k+1=[1+cos2 ![]() ]a2k﹣1+sin2
]a2k﹣1+sin2 ![]() =a2k﹣1+1,即a2k+1﹣a2k﹣1=1.
=a2k﹣1+1,即a2k+1﹣a2k﹣1=1.
所以数列{a2k﹣1}是首项为1、公差为1的等差数列,因此a2k﹣1=k.
当n=2k(k∈N*)时,a2k+2=(1+cos2 ![]() )a2k+sin2
)a2k+sin2 ![]() =2a2k .
=2a2k .
所以数列{a2k}是首项为2、公比为2的等比数列,因此a2k=2k .
该数列的前10项的和为1+2+2+4+3+8+4+16+5+32=77
所以答案是:77
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系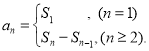 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(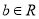 ,
, 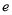 为自然对数的底数)在点
为自然对数的底数)在点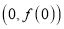 处的切线经过点
处的切线经过点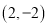 .
.(Ⅰ)讨论函数
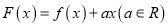 的单调性;
的单调性;(Ⅱ)若
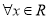 ,不等式
,不等式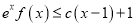 恒成立,求实数
恒成立,求实数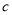 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正数,前n和为Sn , 且Sn=
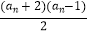 (n∈N*).
(n∈N*).
(1)求证:数列{an}是等差数列;
(2)设bn=an3n , 求数列{bn}的前n项的和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面向量
 ,
,  (
(  ≠
≠  )满足
)满足 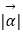 =2,且
=2,且  与
与  ﹣
﹣  的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t)  +t
+t  |的最小值是 . 已知
|的最小值是 . 已知 
 =0,向量
=0,向量  满足(
满足(  ﹣
﹣  )(
)(  ﹣
﹣  )=0,|
)=0,|  ﹣
﹣  |=5,|
|=5,|  ﹣
﹣  |=3,则
|=3,则 
 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】各棱长都等于4的四面ABCD中,设G为BC的中点,E为△ACD内的动点(含边界),且GE∥平面ABD,若
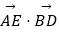 =1,则|
=1,则|  |= .
|= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
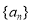 为等差数列,前n项和为
为等差数列,前n项和为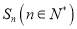 ,
, 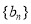 是首项为2的等比数列,且公比大于0,
是首项为2的等比数列,且公比大于0, 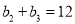 ,
,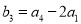 ,
, 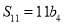 .
.(Ⅰ)求
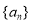 和
和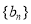 的通项公式;
的通项公式;(Ⅱ)求数列
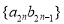 的前n项和
的前n项和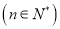 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次不等式ax2+bx+c>0的解集是(﹣
 ,2),则cx2+bx+a<0的解集是( )
,2),则cx2+bx+a<0的解集是( )
A.(﹣3, )
)
B.(﹣∞,﹣3)∪( ,+∞)
,+∞)
C.(﹣2, )
)
D.(﹣∞,﹣2)∪( ,+∞)
,+∞)
相关试题

