【题目】设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为0.
处的切线斜率为0.
(1)求![]() ,
,
(2)若存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)1(2) ![]()
【解析】试题分析:(1)先求出导函数,利用导数的几何意义![]() ,解方程即可的结果;(2)对
,解方程即可的结果;(2)对![]() 分类讨论,当
分类讨论,当![]() 时,当
时,当![]() 时,当
时,当![]() 时,再利用导数研究函数的单调性极值与最值即可得出.
时,再利用导数研究函数的单调性极值与最值即可得出.
试题解析:(1)![]() ,
, ![]() 曲线
曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
, ![]() ,解得
,解得![]() ,综上所述,
,综上所述, ![]() 的值为
的值为![]() .
.
(2)函数![]() 的定义域为
的定义域为![]() ,由(1)可知,
,由(1)可知, ![]() ,
, ![]() .
.
①当![]() 时,则
时,则![]() ,则当
,则当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 存在
存在![]() ,使得
,使得![]() 的充要条件是
的充要条件是![]() ,即
,即![]() ,解得
,解得![]() .
.
②当![]() 时,则
时,则![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 存在
存在![]() ,使得
,使得![]() 充要条件是
充要条件是![]() ,而
,而
![]() ,不符合题意,应舍去.
,不符合题意,应舍去.
③若![]() 时,
时, ![]() ,成立,综上所述,
,成立,综上所述, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =
 ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+2)=f(x﹣2),且当x∈[﹣2,0]时,f(x)=(
 )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
A.(1,2)
B.(2,+∞)
C.(1,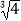 )
)
D.(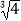 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
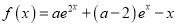
(1)讨论的单调性
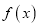 ;
;(2)若
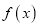 有两个零点,求
有两个零点,求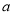 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=
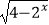 的定义域为A,函数y=lg(x﹣1)(x∈[2,11])的值域为B.
的定义域为A,函数y=lg(x﹣1)(x∈[2,11])的值域为B.
(1)求A和B
(2)求(CRA)∪B. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)为奇函数,当x≥0时,f(x)=
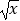 .g(x)=
.g(x)=  ,
,
(1)求当x<0时,函数f(x)的解析式;
(2)求g(x)的解析式,并证明g(x)的奇偶性. -
科目: 来源: 题型:
查看答案和解析>>【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好
总成绩不好
总计
数学成绩好
20
10
30
数学成绩不好
5
15
20
总计
25
25
50
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
相关试题

