【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间.
的单调区间.
(2)当![]() 且
且![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立,求k的最大值.
上恒成立,求k的最大值.
参考答案:
【答案】(1) 增区间为(e﹣3,+∞),减区间为(0,e﹣3)(2)3
【解析】试题分析:(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)分离参数,问题转化为k<![]() 对任意x>1恒成立,根据函数的单调性求出k的最大值即可.
对任意x>1恒成立,根据函数的单调性求出k的最大值即可.
解析:
(1)∵a=2,∴f(x)=2x+xlnx,定义域为(0,+∞),
∴f′(x)=3+lnx,由f′(x)>0得到x>e﹣3,由f′(x)<0得到x<e﹣3,
∴函数f(x)=2x+xlnx的增区间为(e﹣3,+∞),减区间为(0,e﹣3).
(2)当x>1时,x﹣1>0,故不等式k(x﹣1)<f(x)k<![]() ,
,
即k<![]() 对任意x>1恒成立.
对任意x>1恒成立.
令g(x)=![]() ,则g′(x)
,则g′(x)![]() ,
,
令h(x)=x﹣lnx﹣2(x>1),
则h′(x)=1﹣![]() =
=![]() >0h(x)在(1,+∞)上单增.
>0h(x)在(1,+∞)上单增.
∵h(3)=1﹣ln3<0,h(4)=2﹣ln4>0,
∴存在x0∈(3,4)使h(x0)=0,
即当1<x<x0时,h(x)<0,即g′(x)<0,
当x>x0时,h(x)>0,即g′(x)>0,
∴g(x)在(1,x0)上单减,在(x0,+∞)上单增.
令h(x0)=x0﹣lnx0﹣2=0,即lnx0=x0﹣2,
g(x)min=g(x0)=![]() =x0∈(3,4),
=x0∈(3,4),
∴k<g(x)min=x0且k∈Z,
即kmax=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个推理中,属于演绎推理的是( )
A. 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43
B. 观察
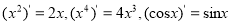 ,可得偶函数的导函数为奇函数
,可得偶函数的导函数为奇函数C. 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8
D. 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
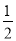 sin 2x-
sin 2x-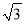 cos2x.
cos2x.(1)求f(x)的周期和最小值;
(2)将函数f(x)的图像上每一点的横坐标伸长到原来的两倍(纵坐标不变),再把所得图像上的所有点向上平移
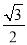 个单位,得到函数g(x)的图像,当
个单位,得到函数g(x)的图像,当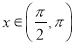 时,求g(x)的值域.
时,求g(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
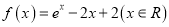 .
.(1)求
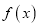 的最小值;
的最小值;(2)求证:x>0时,
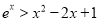 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5 不等式选讲
已知函数f(x)=|x-1|-2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=2m,求ab+bc的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:
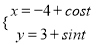 (t为参数),C2:
(t为参数),C2: 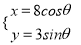 (θ为参数).若曲线C1上的点P对应的参数为t=
(θ为参数).若曲线C1上的点P对应的参数为t=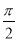 ,Q为曲线C2上的动点,则线段PQ的中点M到直线C3:
,Q为曲线C2上的动点,则线段PQ的中点M到直线C3: 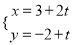 (t为参数)距离的最小值为________.
(t为参数)距离的最小值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l的参数方程为
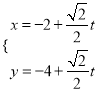 ,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
相关试题

