【题目】已知函数![]() .
.
(Ⅰ)求过点![]() 且与曲线
且与曲线![]() 相切的直线方程;
相切的直线方程;
(Ⅱ)设![]() ,其中
,其中![]() 为非零实数,若
为非零实数,若![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】试题分析:(1)求出![]() 的导数,设出切点,可得切线的斜率,由两点的斜率公式,解方程可得切点坐标,进而得到所求的切线的方程;(2)求出
的导数,设出切点,可得切线的斜率,由两点的斜率公式,解方程可得切点坐标,进而得到所求的切线的方程;(2)求出![]() 解析式和导数,讨论
解析式和导数,讨论![]() ,求出极值点和单调区间,由
,求出极值点和单调区间,由![]() 等价于
等价于![]() ,由
,由![]() 可得
可得![]() ,即证明
,即证明![]()
,由![]() 可得
可得![]() ,即证明
,即证明![]() ,构造函数
,构造函数![]() ,求出导数单调性,即可证。
,求出导数单调性,即可证。
解:(Ⅰ)![]()
设切点为![]() ,则切线的斜率为
,则切线的斜率为![]()
点![]() 在
在![]() 上,
上,![]()
![]() ,解得
,解得![]()
![]() 切线的斜率为
切线的斜率为![]() ,
,![]() 切线方程为
切线方程为![]()
(Ⅱ)![]()
![]()
当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得,
得,![]() ,故
,故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得,
得,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() 有两个极值点,即
有两个极值点,即![]() ,
,
![]() ,由
,由![]() 得,
得,![]()
由![]()
![]() ,即证明
,即证明![]()
即证明![]()
构造函数![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 成立
成立
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
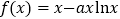 (
(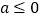 ),
),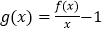 .
.(1)求函数
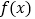 单调区间;
单调区间;(2)当
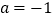 时,
时,①求函数
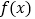 在
在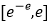 上的值域;
上的值域;②求证:
 ,其中
,其中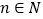 ,
,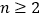 .(参考数据
.(参考数据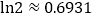 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
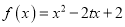 ,
, 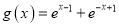 ,且函数
,且函数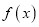 的图象关于直线
的图象关于直线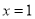 对称。
对称。(1)求函数
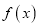 在区间
在区间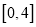 上最大值;
上最大值;(2)设
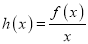 ,不等式
,不等式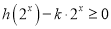 在
在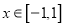 上恒成立,求实数
上恒成立,求实数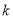 的取值范围;
的取值范围;(3)设
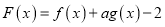 有唯一零点,求实数
有唯一零点,求实数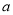 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过
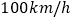 的有20人,不超过
的有20人,不超过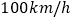 的有10人.在20名女性驾驶员中,平均车速超过
的有10人.在20名女性驾驶员中,平均车速超过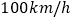 的有5人,不超过
的有5人,不超过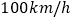 的有15人.
的有15人.(Ⅰ)完成下面的列联表,并判断是否有
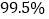 的把握认为平均车速超过
的把握认为平均车速超过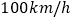 的人与性别有关;
的人与性别有关;平均车数超过
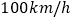 人数
人数平均车速不超过
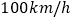 人数
人数合计
男性驾驶员人数
女性驾驶员人数
合计
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随即抽取3辆,记这3辆车中驾驶员为女性且车速不超过
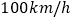 的车辆数为
的车辆数为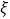 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求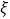 的分布列和数学期望
的分布列和数学期望参考公式:
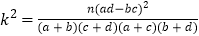 ,其中
,其中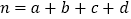 .
.参考数据:
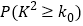
0.150
0.100
0.05
0.025
0.010
0.005
0.001
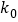
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民自来水收费标准如下:每户每月用水不超过5吨时,每吨为
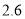 元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费
元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为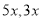 吨。
吨。(1)求
 关于
关于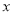 的函数。
的函数。(2)若甲、乙两户该月共交水费
 元,分别求甲、乙两户该月的用水量和水费。
元,分别求甲、乙两户该月的用水量和水费。 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为
 .
.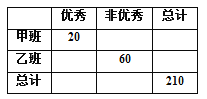
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0)
0.05
0.01
k0
3.841
6.635
附:
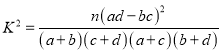
相关试题

