【题目】若f(x)为二次函数,﹣1和3是方程f(x)﹣x﹣4=0的两根,f(0)=1
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>2x+m有解,求实数m的取值范围.
参考答案:
【答案】
(1)解:设二次函数f(x)=ax2+bx+c,(a≠0),
由f(0)=1可得c=1,
故方程f(x)﹣x﹣4=0可化为ax2+(b﹣1)x﹣3=0,
∵﹣1和3是方程f(x)﹣x﹣4=0的两根,
∴由韦达定理可得﹣1+3=﹣ ![]() ,﹣1×3=
,﹣1×3= ![]() ,
,
解得a=1,b=﹣1,故f(x)的解析式为f(x)=x2﹣x+1
(2)解:∵在区间[﹣1,1]上,不等式f(x)>2x+m有解,
∴m<x2﹣3x+1在区间[﹣1,1]上有解,
故只需m小于函数g(x)=x2﹣3x+1在区间[﹣1,1]上的最大值,
由二次函数可知当x=﹣1时,函数g(x)取最大值5,
∴实数m的取值范围为(﹣∞,5)
【解析】(1)设二次函数f(x)=ax2+bx+c,(a≠0),由题意和韦达定理待定系数可得;(2)问题转化为m<x2﹣3x+1在区间[﹣1,1]上有解,只需m小于函数g(x)=x2﹣3x+1在区间[﹣1,1]上的最大值,由二次函数区间的最值可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为
 和
和  .时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线才是底数为e的对数函数的图象.
.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线才是底数为e的对数函数的图象. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y)+
 ,且f(
,且f(  )=0,当x>
)=0,当x>  时,f(x)>0.
时,f(x)>0.
(1)求f(1);
(2)判断函数f(x)的单调性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形
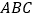 中,若
中,若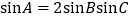 ,则
,则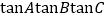 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:
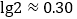 ,
,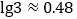 )( )
)( )A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0且a≠1,函数y=a2x+2ax﹣1在[﹣1,1]的最大值是14,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,值域是(0,+∞)的是( )
A.y=( )1﹣x
)1﹣x
B.y=x2
C.y=5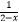
D.y=
相关试题

