【题目】已知x与y之间的几组数据如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得的线性回归方程为![]() =
=![]() x+
x+![]() .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A. ![]() >b′,
>b′,![]() >a′ B.
>a′ B. ![]() >b′,
>b′,![]() <a′
<a′
C. ![]() <b′,
<b′,![]() >a′ D.
>a′ D. ![]() <b′,
<b′,![]() <a′
<a′
参考答案:
【答案】C
【解析】试题分析:由表格总的数据可得n,![]() ,
,![]() ,进而可得
,进而可得![]() ,和
,和![]() ,代入可得
,代入可得![]() ,进而可得
,进而可得![]() ,再由直线方程的求法可得b′和a′,比较可得答案.
,再由直线方程的求法可得b′和a′,比较可得答案.
解:由题意可知n=6,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =
=![]()
![]() =
=![]() ,
,
故![]() =91﹣6×
=91﹣6×![]() =22,
=22,![]() =58﹣6×
=58﹣6×![]() ×
×![]() =
=![]() ,
,
故可得![]() =
=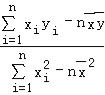 =
=![]() ,
,![]() =
=![]() =
=![]() ﹣
﹣![]() ×
×![]() =
=![]() ,
,
而由直线方程的求解可得b′=![]() =2,把(1,0)代入可得a′=﹣2,
=2,把(1,0)代入可得a′=﹣2,
比较可得![]() <b′,
<b′,![]() >a′,
>a′,
故选C
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把日均收看体育节目的时间超过50分钟的观众称为“超级体育迷”,已知5名“超级体育迷”中有2名女性,若从中任选2名,则至少有1名女性的概率为( )
A.
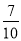 B.
B. 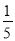
C.
 D.
D. 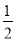
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问110名大学生是否爱好某项运动,得到列联表:
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
由K2=
 ,得K2=
,得K2= ≈7.8.
≈7.8.附表:
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
参照附表,得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个)
10
20
30
加工时间y(分钟)
21
30
39
现已求得上表数据的线性回归方程
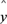 =
=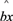 +
+ 中的
中的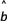 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程
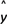 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;③线性回归方程
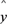 =
=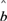 x+
x+ 必过(
必过(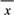 ,
,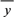 );
);④在一个2×2列联表中,由计算得K2=13.079,则有99%以上的把握认为这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
P(K2≥k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
A. 0 B. 1
C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着经济的发展,某城市的市民收入逐年增长,表1是该城市某银行连续五年的储蓄存款额(年底余额):
表1
年份x
2011
2012
2013
2014
2015
储蓄存款额y(千亿元)
5
6
7
8
10
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 010,z=y-5,得到表2:
表2
时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)z关于t的线性回归方程是________;y关于x的线性回归方程是________;
(2)用所求回归方程预测到2020年年底,该银行储蓄存款额可达________千亿元.
(附:线性回归方程
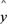 =
=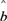 x+
x+ ,其中
,其中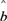 =
=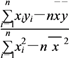 ,
, =
=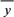 -
-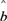
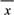 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )

A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
相关试题

