【题目】在平面直角坐标系xoy中,直线l的参数方程为 (t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=4cosθ.
(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=4cosθ.
(1)写出直线l的普通方程和圆C的直角坐标方程.
(2)若点P坐标为(1,1),圆C与直线l交于A,B两点,求|PA|+|PB|的值.
参考答案:
【答案】(1)直线l的普通方程为:x+y﹣2=0,圆C的直角坐标方程为:(x﹣2)2+y2=4.(2)4.
【解析】试题分析:(1)直线l的参数方程为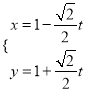 (t为参数).消去参数可得:直线l的普通方程.圆C的方程为ρ=4cosθ.即ρ2=4ρcosθ,利用互化公式可得圆C的直角坐标方程.
(t为参数).消去参数可得:直线l的普通方程.圆C的方程为ρ=4cosθ.即ρ2=4ρcosθ,利用互化公式可得圆C的直角坐标方程.
(2)将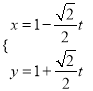 代入(x﹣2)2+y2=4得
代入(x﹣2)2+y2=4得![]() :,利用根与系数的关系可得|PA|+|PB|=|t1﹣t2|=4,
:,利用根与系数的关系可得|PA|+|PB|=|t1﹣t2|=4,
(1)直线l的参数方程为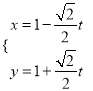 (t为参数).消去参数可得:直线l的普通方程为:x+y﹣2=0,
(t为参数).消去参数可得:直线l的普通方程为:x+y﹣2=0,
圆C的方程为ρ=4cosθ.即ρ2=4ρcosθ,可得圆C的直角坐标方程为:(x﹣2)2+y2=4.
(2)将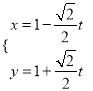 代入(x﹣2)2+y2=4得:
代入(x﹣2)2+y2=4得: ![]() ,
,
得![]() 则
则![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=
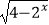 的定义域为A,函数y=lg(x﹣1)(x∈[2,11])的值域为B.
的定义域为A,函数y=lg(x﹣1)(x∈[2,11])的值域为B.
(1)求A和B
(2)求(CRA)∪B. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)为奇函数,当x≥0时,f(x)=
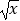 .g(x)=
.g(x)=  ,
,
(1)求当x<0时,函数f(x)的解析式;
(2)求g(x)的解析式,并证明g(x)的奇偶性. -
科目: 来源: 题型:
查看答案和解析>>【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好
总成绩不好
总计
数学成绩好
20
10
30
数学成绩不好
5
15
20
总计
25
25
50
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,
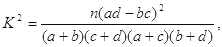 其中
其中 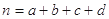 为样本容量。
为样本容量。P(K2≥k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)根据以上数据建立一个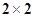 的列联表;
的列联表;
(2)试判断是否有95%的把握认为是否晕机与性别有关? -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“ 25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:
 ,
,  ,
,  ,
,  ,
,  分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

附表:P(
 )
)0.100
0 .010
0.001
k
2.706
6.635
10.828
 ,(其中
,(其中  )
)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 的列联表,并判断是否有
的列联表,并判断是否有  的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段






男
3
9
18
15
6
9
女
6
4
5
10
13
2
附表及公式:

0.100
0.050
0.010
0.001
k
2.706
3.841
6.635
10.828

(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
相关试题

