【题目】函数![]() ,
,![]() .
.
(Ⅰ)讨论![]() 的极值点的个数;
的极值点的个数;
(Ⅱ)若对于![]() ,总有
,总有![]() .(i)求实数
.(i)求实数![]() 的范围; (ii)求证:对于
的范围; (ii)求证:对于![]() ,不等式
,不等式![]() 成立.
成立.
参考答案:
【答案】见解析.
【解析】【试题分析】(Ⅰ)先运用求导法则求函数的导数,再分类进行探求; (Ⅱ)先将不等式进行等价转化,再构造函数借助导数的有关知识进行推证:
(Ⅰ)解法一:由题意得![]() , 令
, 令![]()
(1)当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 恒成立
恒成立
即![]() 对
对![]() 恒成立,此时
恒成立,此时![]() 没有极值点;…………2分
没有极值点;…………2分
(2)当![]() ,即
,即![]()
①![]() 时,设方程
时,设方程![]() 两个不同实根为
两个不同实根为![]() ,不妨设
,不妨设![]()
则![]() ,故
,故![]()
∴![]() 时
时![]() ;在
;在![]() 时
时![]()
故![]() 是函数
是函数![]() 的两个极值点.
的两个极值点.
②![]() 时,设方程
时,设方程![]() 两个不同实根为
两个不同实根为![]() ,
,
则![]() ,故
,故![]()
∴![]() 时,
时,![]() ;故函数
;故函数![]() 没有极值点. ……………………………4分
没有极值点. ……………………………4分
综上,当![]() 时,函数
时,函数![]() 有两个极值点;
有两个极值点;
当![]() 时,函数
时,函数![]() 没有极值点. ………………………………………5分
没有极值点. ………………………………………5分
解法二:![]() , …………………………………………1分
, …………………………………………1分
![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,![]() 在
在![]() 单调增,
单调增,![]() 没有极值点; ……………………………………………………………3分
没有极值点; ……………………………………………………………3分
②当![]() ,即
,即![]() 时,方程
时,方程![]() 有两个不等正数解
有两个不等正数解![]() ,
,
![]()
不妨设![]() ,则当
,则当![]() 时,
时,![]() 增;
增;![]() 时,
时,![]() 减;
减;![]() 时,
时,![]() 增,所以
增,所以![]() 分别为
分别为![]() 极大值点和极小值点,
极大值点和极小值点,![]() 有两个极值点.
有两个极值点.
综上所述,当![]() 时,
时,![]() 没有极值点;
没有极值点;
当![]() 时,
时,![]() 有两个极值点. ………………………………5分
有两个极值点. ………………………………5分
(Ⅱ)(i)![]() ,
,
由![]() ,即
,即![]() 对于
对于![]() 恒成立,设
恒成立,设![]() ,
,
![]() ,
,
![]() ,
,![]() 时,
时,![]() 减,
减,![]() 时,
时,![]() 增,
增,
![]() ,
,![]() . ……………………………………9分
. ……………………………………9分
(ii)由(i)知,当![]() 时有
时有![]() ,即:
,即:![]() ,
,![]() ……①当且仅当
……①当且仅当![]() 时取等号, ……………………………10分
时取等号, ……………………………10分
以下证明:![]() ,设
,设![]() ,
,![]() ,
,
![]() 当
当![]() 时
时![]() 减,
减,![]() 时
时![]() 增,
增,
![]() ,
,![]() ,……②当且仅当
,……②当且仅当![]() 时取等号;
时取等号;
由于①②等号不同时成立,故有![]() .……………………………12分
.……………………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
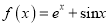 (
(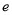 为自然对数的底数),
为自然对数的底数),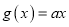 ,
, 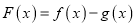 .
.(1)若
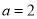 ,且直线
,且直线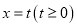 分别与函数
分别与函数 和
和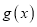 的图象交于
的图象交于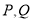 ,求
,求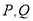 两点间的最短距离;
两点间的最短距离; (2)若
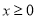 时,函数
时,函数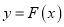 的图象恒在
的图象恒在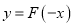 的图象上方,求实数
的图象上方,求实数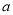 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中,a1=1,an+an+1=(
 )n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= .
)n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= . -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代一部重要的数学著作,书中给出了如下问题:“今有良马与驽马发长安,至齐,齐去长安一千一百二十五里.良马初日行一百零三里,日增一十三里,驽马初日行九十七里,日减半里,良马先至齐,复还迎驽马,问几何日相逢?”其大意:“现有良马和驽马同时从长安出发到齐去,已知长安和齐的距离是
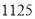 里.良马第一天走
里.良马第一天走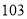 里,之后每天比前一天多走
里,之后每天比前一天多走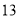 里.驽马笫一天走
里.驽马笫一天走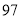 里,之后每天比前一天少走
里,之后每天比前一天少走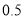 里.良马到齐后,立刻返回去迎驽马,多少天后两马相遇?”在这个问题中驽马从出发到相遇行走的路程为__________ 里.
里.良马到齐后,立刻返回去迎驽马,多少天后两马相遇?”在这个问题中驽马从出发到相遇行走的路程为__________ 里. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
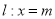 (
(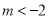 )与
)与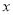 轴交于
轴交于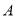 点,动圆
点,动圆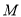 与直线
与直线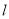 相切,并且与圆
相切,并且与圆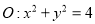 相外切,
相外切,(1)求动圆的圆心
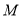 的轨迹
的轨迹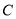 的方程;
的方程;(2)若过原点且倾斜角为
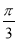 的直线与曲线
的直线与曲线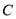 交于
交于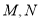 两点,问是否存在以
两点,问是否存在以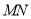 为直径的圆经过点
为直径的圆经过点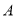 ?若存在,求出
?若存在,求出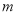 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式为12x2﹣ax>a2 .
(1)当a=2时,求不等式的解集;
(2)当a∈R时,求不等式的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两条直线l1(3+m)x+4y=5﹣3m,l2 2x+(5+m)y=8.当m分别为何值时,l1与l2:
(1)相交?
(2)平行?
(3)垂直?
相关试题

