【题目】某集团为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查投入广告费t(百万元),可增加销售额约为-t2+5t(百万元)(0≤t≤5) (注:收益=销售额-投放).
(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-![]() x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大.
参考答案:
【答案】将2百万元用于技术改造, 1百万元用于广告促销,该公司由此获得的收益最大.
【解析】试题分析:(1)设投入![]() 百万元)的广告费后增加的收益为
百万元)的广告费后增加的收益为![]() ,根据收益为销售额与投放的差可建立收益模型为:
,根据收益为销售额与投放的差可建立收益模型为: ![]() ,再由二次函数法求得最大值;(2)根据题意,若用技术改造的资金为
,再由二次函数法求得最大值;(2)根据题意,若用技术改造的资金为![]() (百万元),则用于广告促销的资金为
(百万元),则用于广告促销的资金为![]() (百万元),则收益模型为
(百万元),则收益模型为![]() ,因为是高次函数,所以用导数法研究其最大值.
,因为是高次函数,所以用导数法研究其最大值.
试题解析:(1)设投入t(t百万元)的广告费后增加的收益为f(t)(百万元),
则有f(t)=(-t2+5t)-t=-t2+4t=-(t-2) 2+4(0<t≤3),
所以当t=2百万元时,f(t)取得最大值4百万元.
即投入2百万元时的广告费时,该公司由此获得的收益最大.
(2)设用技术改造的资金为x(百万元),则用于广告促销的资金为(3-x)(百万元),则
则有g(x)=![]() +[-(3-x)2+5(3-x)]-3=-
+[-(3-x)2+5(3-x)]-3=-![]() x3+4x+3(0≤x≤3)
x3+4x+3(0≤x≤3)
所以g′(x)=-x2+4.令g′(x)=0,解得x=2,或x=-2(舍去).
又当0≤x<2时,g′ (x)>0,当2<x≤3时,g′(x)<0.
故g(x)在[0,2]上是增函数,在[2,3]上是减函数.
所以当x=2时,g(x)取最大值,
即将2百万元用于技术改造, 1百万元用于广告促销,该公司由此获得的收益最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面
 平面
平面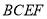 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形,  ,
, 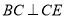 ,
, 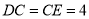 ,
, 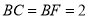 .
.
(1)求证:
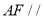 平面
平面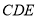 ;
;(2)求直线
 与平面
与平面 所成角的余弦值;
所成角的余弦值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
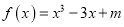 ,若在区间
,若在区间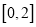 上任取三个数
上任取三个数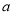 、
、 、
、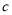 ,均存在以
,均存在以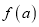 、
、 、
、 为边长的三角形,则实数
为边长的三角形,则实数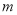 的取值范围为__________.
的取值范围为__________. -
科目: 来源: 题型:
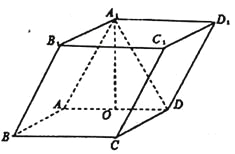
查看答案和解析>>【题目】如图,四棱柱
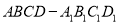 中,底面
中,底面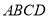 是矩形,且
是矩形,且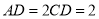 ,
, 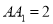 ,
, 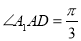 ,若
,若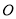 为
为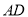 的中点,且
的中点,且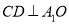 .
.
(Ⅰ)求证:
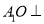 平面
平面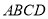 ;
;(Ⅱ)线段
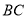 上是否存在一点
上是否存在一点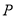 ,使得二面角
,使得二面角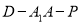 的大小为
的大小为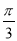 ?若存在,求出
?若存在,求出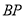 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
相关试题

