【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在![]() 处的投中率
处的投中率![]() ,在
,在![]() 处的投中率为
处的投中率为![]() ,该同学选择先在
,该同学选择先在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)该同学选择都在
;(3)该同学选择都在![]() 处投篮得分超过
处投篮得分超过![]() 分的概率大.
分的概率大.
【解析】
试题分析:对问题(1)根据题目条件并结合所给的分布列以及独立重复试验同时发生的概率计算方法,即可求得![]() 的值;对问题(2),根据问题(1)的结论并结合
的值;对问题(2),根据问题(1)的结论并结合![]() 取各个值的几何意义,即可求得随机变量
取各个值的几何意义,即可求得随机变量![]() 的数学期望
的数学期望![]() ;对问题(3)根据题目的要求可先求出都在
;对问题(3)根据题目的要求可先求出都在![]() 处投篮得分超过
处投篮得分超过![]() 分的概率以及选择上述方式投篮得分超过
分的概率以及选择上述方式投篮得分超过![]() 分的概率,进而可比较概率的大小.
分的概率,进而可比较概率的大小.
试题解析:(1)设该同学在![]() 处投中为事件
处投中为事件![]() ,在
,在![]() 处投中为事件
处投中为事件![]() ,
,
则事件![]() 相互独立,且
相互独立,且![]() ,
,
根据分布列知:![]() 时,
时,![]() ,
,
所以![]()
(2)当![]() 时,
时,![]()
![]() .
.
当![]() 时,
时,![]()
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() .
.
所以随机变量![]() 的分布列为
的分布列为
| 0 | 2 | 3 | 4 | 5 |
| 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
∴随机变量![]() 的数学期望:
的数学期望:
![]() .
.
(3)该同学选择都在![]() 处投篮得分超过3分的概率为
处投篮得分超过3分的概率为
![]() .
.
该同学选择(1)中方式投篮得分超过3分的概率为![]() ,
,
所以该同学选择都在![]() 处投篮得分超过3分的概率大
处投篮得分超过3分的概率大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)设
 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于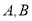 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个.从中任取一球,得到红球的概率是
 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是 ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是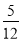 .
.(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是“红球或绿球”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数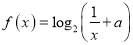 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若关于
 的方程
的方程 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间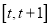 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果想用统计图来反映各数据的变化趋势,比较合适的统计图是( )
A.条形图B.折线图C.扇形图D.其他图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查方式中合适的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取
 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位: ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
(1)求
 、
、 、
、 及
及 、
、 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);(2)已知标准乒乓球的直径为
 ,直径误差不超过
,直径误差不超过 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;(3)统计方法中,同一组数据常用该组区间的中点值(例如区间
 的中点值是
的中点值是 )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数.
相关试题

