【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个.从中任取一球,得到红球的概率是![]() ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是![]() ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是![]() .
.
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是“红球或绿球”的概率.
参考答案:
【答案】(1)![]() 、
、![]() 、
、![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1) 记事件![]() “得到红球”,事件
“得到红球”,事件![]() “得到黑球”,事件
“得到黑球”,事件![]() “得到黄球”,事件
“得到黄球”,事件![]() “得到绿球”,由事件
“得到绿球”,由事件![]() 、
、![]() 、
、![]() 、
、![]() 两两互斥,列出方程组,即可求解求得到黑球、黄球、绿球的概率;(2)事件“得到红球或绿球”可表示为事件“
两两互斥,列出方程组,即可求解求得到黑球、黄球、绿球的概率;(2)事件“得到红球或绿球”可表示为事件“![]() ”,由(1)及互斥事件概率加法公式,即可求解不是“红球或绿球”的概率.
”,由(1)及互斥事件概率加法公式,即可求解不是“红球或绿球”的概率.
试题解析:(1)从![]() 个球中任取一个,记事件
个球中任取一个,记事件![]() “得到红球”,事件
“得到红球”,事件![]() “得到黑球”,事件
“得到黑球”,事件![]() “得到黄球”,事件
“得到黄球”,事件![]() “得到绿球”,则事件
“得到绿球”,则事件![]() 、
、![]() 、
、![]() 、
、![]() 两两互斥,
两两互斥,
由题意有: 即
即
解之,得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故得到黑球、黄球、绿球的概率分别为![]() 、
、![]() 、
、![]() .
.
(2)事件“得到红球或绿球”可表示为事件“![]() ”,由(1)及互斥事件概率加法公式得:
”,由(1)及互斥事件概率加法公式得:
![]() ,
,
故得到的不是“红球或绿球”的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧棱
中,侧棱 ,底面
,底面 为直角梯形,其中
为直角梯形,其中 ,
, .
.
(1)求证:侧面PAD⊥底面ABCD;
(2)求三棱锥
 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( ).
).(1)求直线
 经过的定点坐标;
经过的定点坐标;(2)若直线
 交
交 负半轴于
负半轴于 ,交
,交 轴正半轴于
轴正半轴于 ,
, 为坐标系原点,
为坐标系原点, 的面积为
的面积为 ,求
,求 的最小值并求此时直线
的最小值并求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)设
 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于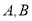 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数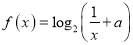 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若关于
 的方程
的方程 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间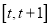 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在
 处每投进一球得3分;在
处每投进一球得3分;在 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为 ,该同学选择先在
,该同学选择先在 处投第一球,以后都在
处投第一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
0
2
3
4
5

0.03




(1)求
 的值;
的值;(2)求随机变量
 的数学期望
的数学期望 ;
;(3)试比较该同学选择上述方式投篮得分超过3分与选择都在
 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果想用统计图来反映各数据的变化趋势,比较合适的统计图是( )
A.条形图B.折线图C.扇形图D.其他图形
相关试题

