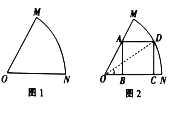
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]()
![]() (
(![]() );(3)
);(3)![]() .
.
【解析】试题分析:(1)直角三角形中,根据锐角三角函数的定义即可表示出![]() 的值;(2 )求出
的值;(2 )求出![]() ,代入面积公式得出S关于
,代入面积公式得出S关于![]() 的函数;(3)利用二倍角公式及辅助角公式,三角恒等变换化简
的函数;(3)利用二倍角公式及辅助角公式,三角恒等变换化简![]() ,根据的
,根据的![]() 范围和正弦函数的性质即可得出S的最大值.
范围和正弦函数的性质即可得出S的最大值.
试题解析:(1)因为![]() ,四边形
,四边形![]() 是矩形,
是矩形,
所以在![]() 中,
中, ![]() .
.
所以![]() .
.
在![]() 中,
中, 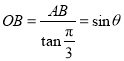 .
.
(2)在![]() 中,
中, ![]() .
.
所以![]() .
.
所以![]()
![]()
![]() (
(![]() ).
).
(3)因为![]()
![]() ,
,
![]()
![]() (
(![]() ),
),
所以,当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
【方法点晴】本题考查的知识点比较多,主要考查等比数列的定义、余弦定理及三角函数的最值,属于难题.求与三角函数有关的最值常用方法有以下几种:①化成![]() 的形式利用配方法求最值;②形如
的形式利用配方法求最值;②形如![]() 的可化为
的可化为![]() 的形式利用三角函数有界性求最值;③
的形式利用三角函数有界性求最值;③![]() 型,可化为
型,可化为![]() 求最值 .本题(3)是利用方法③的思路解答的.
求最值 .本题(3)是利用方法③的思路解答的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至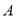 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的 处有一外国船只,且
处有一外国船只,且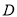 岛位于海监船正东
岛位于海监船正东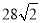 海里处.
海里处.
(1)求此时该外国船只与
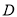 岛的距离;
岛的距离;(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离
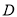 岛24海里处,不让其进入
岛24海里处,不让其进入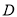 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据: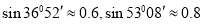 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型
特大套
大套
经济适用房
舒适
100
150

标准
300
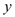
600
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求
 ,
,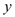 的值;
的值;(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
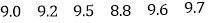
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为
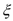 ,求
,求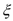 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
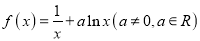 .
.(1)若
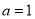 ,求函数
,求函数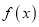 的极值和单调区间;
的极值和单调区间;(2)若在区间
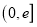 上至少存在一点
上至少存在一点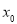 ,使得
,使得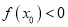 成立,求实数
成立,求实数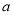 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在
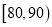 之间的男生人数;
之间的男生人数;(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在
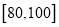 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自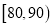 、
、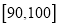 的概率.
的概率.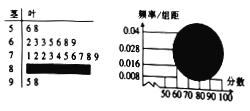
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
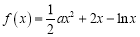 .
.(1)若
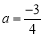 ,判断函数
,判断函数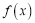 的单调性;
的单调性;(2)若函数
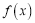 在定义域内单调递减,求实数
在定义域内单调递减,求实数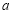 的取值范围;
的取值范围;(3)当
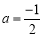 时,关于
时,关于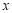 的方程
的方程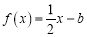 在
在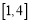 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数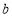 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
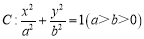 的左、右焦点分别为
的左、右焦点分别为 ,
, ,椭圆上一点
,椭圆上一点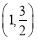 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于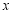 轴.
轴.(1)求椭圆
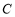 的方程;
的方程;(2)与抛物线
 相切于第一象限的直线
相切于第一象限的直线 ,与椭圆
,与椭圆 交于
交于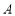 ,
, 两点,与
两点,与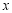 轴交于点
轴交于点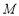 ,线段
,线段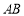 的垂直平分线与
的垂直平分线与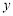 轴交于点
轴交于点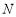 ,求直线
,求直线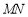 斜率的最小值.
斜率的最小值.
相关试题

