【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求得函数的导数,可得切线的斜率和切点,由点斜式方程可得切线方程;(2)函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,可得
,可得![]() 在
在![]() 上恒成立,可令
上恒成立,可令![]() ,由
,由![]() 且
且![]() ,解不等式即可得到所求范围.
,解不等式即可得到所求范围.
试题解析:(1)![]() ,
,
![]() ,所以所求切线的方程为:
,所以所求切线的方程为: ![]()
即![]() ;
;
(2)因为函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
令![]() ,则需
,则需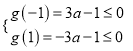 ,
,
所以![]() ,即
,即![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线以及利用导数研究函数的单调性,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为
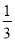 ,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________.
,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________. -
科目: 来源: 题型:
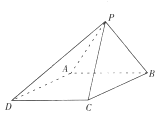
查看答案和解析>>【题目】如图,已知四棱锥
 的底面为菱形,
的底面为菱形, 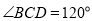 ,
, 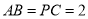 ,
, 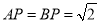 .
.
(Ⅰ)求证:
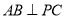 ;
;(Ⅱ)求二面角
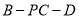 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于二项式(x-1)2005有下列命题:
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为
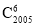 x1999;
x1999;③该二项展开式中系数最大的项是第1002项;
④当x=2006时,(x-1)2005除以2006的余数是2005。
其中正确命题的序号是__________。(注:把你认为正确的命题序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
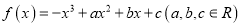 在区间
在区间 内单调递减,在区间
内单调递减,在区间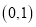 内单调递增,且
内单调递增,且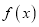 在
在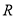 上有三个零点,1是其中一个零点.
上有三个零点,1是其中一个零点.(1)求
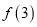 的取值范围;
的取值范围;(2)若直线
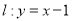 在曲线
在曲线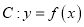 的上方部分所对应的
的上方部分所对应的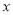 的集合为
的集合为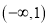 ,试求实数
,试求实数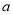 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
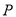 是长轴长为
是长轴长为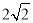 的椭圆
的椭圆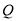 :
: 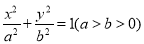 上异于顶点的一个动点,
上异于顶点的一个动点,  为坐标原点,
为坐标原点,  为椭圆的右顶点,点
为椭圆的右顶点,点 为线段
为线段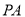 的中点,且直线
的中点,且直线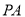 与
与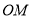 的斜率之积恒为
的斜率之积恒为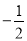 .
.(1)求椭圆
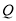 的方程;
的方程;(2)设过左焦点
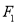 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线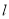 交椭圆于
交椭圆于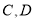 两点,线段
两点,线段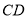 的垂直平分线与
的垂直平分线与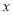 轴交于点
轴交于点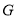 ,点
,点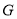 横坐标的取值范围是
横坐标的取值范围是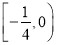 ,求
,求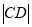 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
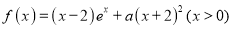 .
.(1)若
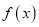 是
是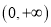 的单调递增函数,求实数
的单调递增函数,求实数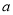 的取值范围;
的取值范围;(2)当
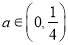 时,求证:函数
时,求证:函数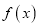 有最小值,并求函数
有最小值,并求函数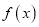 最小值的取值范围.
最小值的取值范围.
相关试题

