【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的单调递增函数,求实数
的单调递增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求证:函数
时,求证:函数![]() 有最小值,并求函数
有最小值,并求函数![]() 最小值的取值范围.
最小值的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)函数单调递增等价于导函数![]() ,再利用变量分离转化为求对应函数最值问题:
,再利用变量分离转化为求对应函数最值问题: ![]() 的最大值,最后根据导数求对应函数最值,即得实数
的最大值,最后根据导数求对应函数最值,即得实数![]() 的取值范围;(2)实质证明函数
的取值范围;(2)实质证明函数![]() 当
当![]() 时先减后增,也即函数有极小值点,并在此极小值点处取最小值,此时要用零点存在定理说明极值点存在.求出函数极小值表达式,即最小值表达式,利用导数研究最小值表达式单调性,并根据极小值点范围确定最小值取值范围.
时先减后增,也即函数有极小值点,并在此极小值点处取最小值,此时要用零点存在定理说明极值点存在.求出函数极小值表达式,即最小值表达式,利用导数研究最小值表达式单调性,并根据极小值点范围确定最小值取值范围.
试题解析:(Ⅰ) ![]()
∵函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() . ∴
. ∴![]() ,∴
,∴![]() ,
,
令![]() ,
, 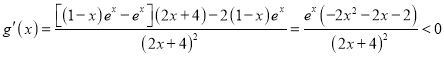 ,
,
∴![]() ,∴
,∴![]() .
.
(Ⅱ)![]() ∴
∴![]()
![]()
![]() ∴
∴![]()
∴![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,∴
,∴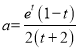 .
.
由(Ⅰ)知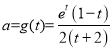 在
在![]() 上单调递减,
上单调递减,
![]() ,且
,且![]() ,∴
,∴![]() .
.
∴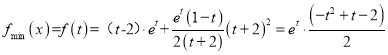 ,
,
![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 的最小值的取值范围是
的最小值的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
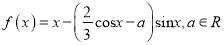 .
.(1)求曲线
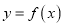 在点
在点 处的切线方程;
处的切线方程;(2)若函数
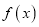 在
在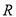 上单调递增,求实数
上单调递增,求实数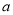 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
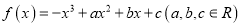 在区间
在区间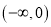 内单调递减,在区间
内单调递减,在区间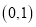 内单调递增,且
内单调递增,且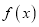 在
在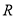 上有三个零点,1是其中一个零点.
上有三个零点,1是其中一个零点.(1)求
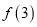 的取值范围;
的取值范围;(2)若直线
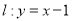 在曲线
在曲线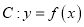 的上方部分所对应的
的上方部分所对应的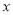 的集合为
的集合为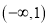 ,试求实数
,试求实数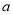 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
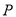 是长轴长为
是长轴长为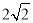 的椭圆
的椭圆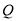 :
: 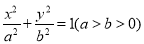 上异于顶点的一个动点,
上异于顶点的一个动点, 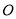 为坐标原点,
为坐标原点, 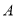 为椭圆的右顶点,点
为椭圆的右顶点,点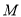 为线段
为线段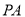 的中点,且直线
的中点,且直线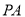 与
与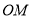 的斜率之积恒为
的斜率之积恒为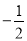 .
.(1)求椭圆
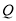 的方程;
的方程;(2)设过左焦点
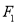 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线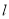 交椭圆于
交椭圆于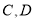 两点,线段
两点,线段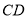 的垂直平分线与
的垂直平分线与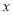 轴交于点
轴交于点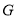 ,点
,点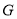 横坐标的取值范围是
横坐标的取值范围是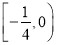 ,求
,求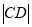 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
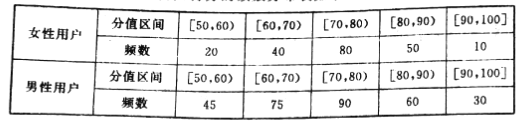
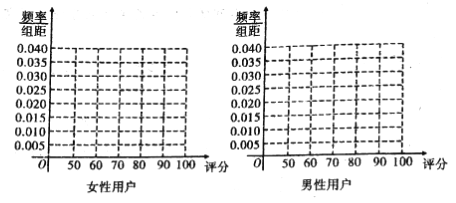
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
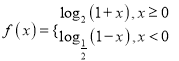 .
.(1)判断函数
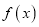 的奇偶性;
的奇偶性;(2)对任意两个实数
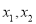 ,求证:当
,求证:当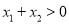 时,
时, 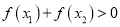 ;
;(3)对任何实数
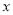 ,
, 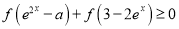 恒成立,求实数
恒成立,求实数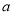 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
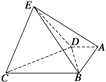
(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
相关试题

