【题目】已知函数 ![]() 是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
参考答案:
【答案】C
【解析】解:由 ![]() 得g′(x)=x2+1﹣
得g′(x)=x2+1﹣ ![]() .
.
∵g(x)是[1,+∞)上的增函数,∴g′(x)≥0在[1,+∞)上恒成立,即x2+1﹣ ![]() ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立.
设x2=t,∵x∈[1,+∞),∴t∈[1,+∞),即不等式t+1﹣ ![]() ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立.
设y=t+1﹣ ![]() ,t∈[1,+∞),
,t∈[1,+∞),
∵y′=1+ ![]() >0,
>0,
∴函数y=t+1﹣ ![]() 在[1,+∞)上单调递增,因此ymin=2﹣m.
在[1,+∞)上单调递增,因此ymin=2﹣m.
∵ymin≥0,∴2﹣m≥0,即m≤2.又m>0,故0<m≤2.m的最大值为2.
故得g(x)= ![]() x3+x﹣2+
x3+x﹣2+ ![]() ,x∈(﹣∞,0)∪(0,+∞).
,x∈(﹣∞,0)∪(0,+∞).
将函数g(x)的图象向上平移2个长度单位,所得图象相应的函数解析式为φ(x)= ![]() x3+2x+
x3+2x+ ![]() ,x∈(﹣∞,0)∪(0,+∞).
,x∈(﹣∞,0)∪(0,+∞).
由于φ(﹣x)=﹣φ(x),
∴φ(x)为奇函数,
故φ(x)的图象关于坐标原点成中心对称.
由此即得函数g(x)的图象关于点Q(0,﹣2)成中心对称.
这表明存在点Q(0,﹣2),使得过点Q的直线若能与函数g(x)的图象围成两个封闭图形,则这两个封闭图形的面积总相等.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从椭圆
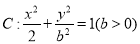 上一点
上一点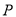 向
向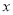 轴作垂线,垂足恰好为椭圆的左焦点
轴作垂线,垂足恰好为椭圆的左焦点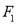 ,
,  是椭圆的右顶点,
是椭圆的右顶点, 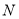 是椭圆的上顶点,且
是椭圆的上顶点,且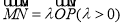 .
.(1)求该椭圆
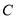 的方程;
的方程;(2)不过原点的直线
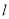 与椭圆
与椭圆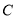 交于
交于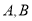 两点,已知
两点,已知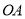 ,直线
,直线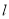 ,
, 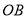 的斜率
的斜率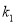 ,
, 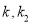 成等比数列,记以
成等比数列,记以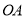 ,
, 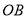 为直径的圆的面积分别为
为直径的圆的面积分别为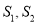 ,求证;
,求证; 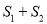 为定值,并求出定值.
为定值,并求出定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
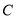 与直线
与直线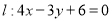 相切于点
相切于点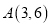 ,且经过点
,且经过点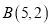 ,求圆
,求圆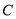 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
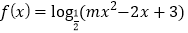 。
。(1)若f(x)在
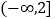 上为增函数,求m的取值范围;
上为增函数,求m的取值范围;(2)若f(x)的值域为R,求m的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 .
.(1)若
 ,求
,求 的概率;
的概率;(2)若
 ,求
,求 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知λ∈R,函数
 g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义max{a,b}表示实数a,b中的较大的数.已知数列{an}满足a1=a(a>0),a2=1,an+2=
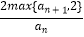 (n∈N),若a2015=4a,记数列{an}的前n项和为Sn , 则S2015的值为 .
(n∈N),若a2015=4a,记数列{an}的前n项和为Sn , 则S2015的值为 .
相关试题

